 2016/7/26
2016/7/26  三角比・三角関数
三角比・三角関数
$2$ 倍角の公式の $3$ 通りの証明を紹介します.
$2$ 倍角の公式 (または倍角の公式) とは,次の公式のことです.
$2$ 倍角の公式:
$$\large \sin 2\theta=2\sin \theta \cos \theta$$ $$\large \cos 2\theta=\cos^2 \theta-\sin^2 \theta$$ $$\large \tan 2\theta= \frac{2\tan \theta}{1-\tan^2 \theta}$$
$2\theta$ の正弦,余弦,正接は,いずれも $\theta$ の正弦,余弦,正接などで表すことができるという主張です.この等式は $\theta$ がどのような値のときも成り立ちます.(ただし,$\theta=\frac{\pi}{4}+\frac{m}{2}\pi$,($m$ は整数)のときは,$\tan 2\theta$ が取る値はないので,$\tan$ の式は考えない.) もし,$\sin 2\theta=2\sin \theta \cos \theta$ と,$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$ が成り立つことを仮定すると,$\theta \neq \frac{\pi}{4}+\frac{m}{2}\pi$ (ただし,$m$ は整数) のとき, $$\tan 2\theta=\frac{\sin 2\theta}{\cos 2\theta}$$ より, $$\tan 2\theta=\frac{2\sin \theta \cos \theta}{\cos^2 \theta-\sin^2 \theta}=\frac{2\tan \theta}{1-\tan^2 \theta}$$ が示せます.つまり,$\sin $ と $\cos$ の倍角の公式から $\tan$ の倍角の公式はただちに導かれるのでわざわざ覚える必要はありません.
以下では $\sin $ と $\cos$ の $2$ 倍角の公式についてのみ考えます.
最も標準的な証明は,加法定理を用いる証明です.$2$ 倍角の公式は以下の証明を見ればわかるように,加法定理からただちに導けるので必ずしも覚える必要はありません.とはいっても,$2$ 倍角の公式は頻繁に用いられるので,自然と覚えてしまうとは思いますが.
$2$ 倍角の公式の証明: $$\sin 2\theta=\sin (\theta+\theta)=\sin\theta\cos \theta+\cos \theta\sin \theta (加法定理より)$$ $$=2\sin \theta\cos \theta$$ $$\cos 2\theta=\cos (\theta+\theta)=\cos\theta\cos\theta-\sin\theta\sin\theta (加法定理より)$$ $$=\cos^2 \theta-\sin^2 \theta$$
$2$ 倍角の公式は,ド・モアブルの定理を用いても導くことができます.ド・モアブルの定理を用いると,$\sin$ と $\cos$ の公式を同時に得ることができます.
$2$ 倍角の公式の証明: ド・モアブルの定理より, $$(\cos \theta+i\sin \theta)^2=\cos 2\theta+i\sin 2\theta \cdots (1)$$ また,上の等式の左辺を展開すると, $$(\cos \theta+i\sin \theta)^2=(\cos^2 \theta-\sin^2 \theta)+i(2\sin \theta\cos \theta) \cdots (2)$$ 式 $(1)$ と $(2)$ の実部と虚部をそれぞれ比較すると, $$\sin 2\theta=2\sin \theta \cos \theta$$ $$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$$ が得られる.
$0 < \theta
$\sin 2\theta=2\sin \theta \cos \theta$ の証明
以下の図のように,半径 $1$ の円の直径を斜辺にもつような直角三角形 $ABC$ を考えます.$\angle BAC=\theta$ とすると,円周角の定理より,$\angle BOC=2\theta$ です.
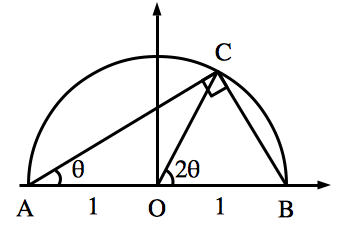 さらに,$AC=2\cos \theta$,$BC=2\sin \theta$ です.ここで, $C$ から $AB$ へ垂線を下ろしその足を $D$ とします.そして,線分 $CD$ の長さを $2$ 通りの方法で計算します.
さらに,$AC=2\cos \theta$,$BC=2\sin \theta$ です.ここで, $C$ から $AB$ へ垂線を下ろしその足を $D$ とします.そして,線分 $CD$ の長さを $2$ 通りの方法で計算します.
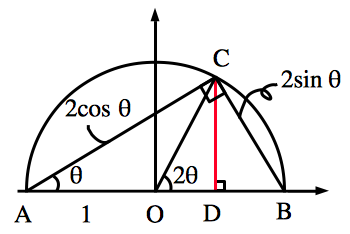
まず,$△ACD$ に着目すると,$CD=2\sin \theta\cos \theta$ です. 続いて,$△OCD$ に着目すると,$CD=\sin 2\theta$ です.
よって,$\sin 2\theta=2\sin \theta \cos \theta$ が成り立ちます.
$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$の証明
先ほどの図を引き続き用います.$OD=\cos 2\theta$ なので,線分 $OD$ を別の方法で表すことを考えます.ここで,$O$ から $BC$ に垂線を下ろしその足を $E$ とし,さらに,$E$ から $AB$ に垂線を下ろしその足を $F$ とします.すると,$OD=OF-DF$ ですが,実は,$OF-DF=\cos^2\theta-\sin^2\theta$ となるのです.以下,それを示します.
まず,$△OBC$ は $OB=OC$ の二等辺三角形であることに注意してください. $O$ は $AB$ の中点,$E$ は $BC$ の中点なので,中点連結定理より, $$OE=\frac{1}{2}AC=\cos \theta$$ です.したがって,$OF=\cos^2 \theta$ です. さらに,$△CBD$ に着目すると,$E$ が $BC$ の中点であることと,$CD // EF$ より, $F$ は $DB$ の中点.また,三角形の相似から,$\angle BEF=\theta$ であることがわかるので, $$DF=FB=EB\sin \theta=\sin^2\theta$$ よって,$\cos 2\theta=\cos^2 \theta-\sin^2 \theta$ が成り立ちます.
このようにして,$\theta$ の範囲が限定的ではありますが,図形的に証明することもできます.
