三角形の内角・外角の二等分線の性質は，中学数学で習う基本的で重要な性質です．それらの主張とその証明を紹介します．さらに，後半では発展的内容として，角の二等分線の長さについても紹介します．
三角形のひとつの角の二等分線が与えられたとき，次の基本的な比の関係式が成り立ちます．
三角形の内角の二等分線と比： $△ ABC$ の $\angle A$ の内角の二等分線と辺 $BC$ との交点を $D$ とする．このとき，次の関係式が成り立つ． $$\large AB:AC=BD:DC$$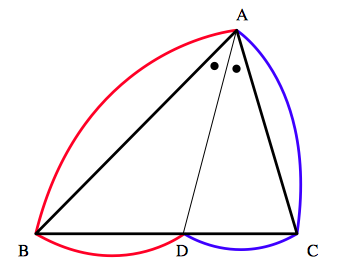 
この事実は二等辺三角形の性質と，平行線と比の性質を用いて証明することができます．
証明： 点 $C$ を通り直線 $AD$ に平行な直線と，$BA$ の延長との交点を $E$ とする．
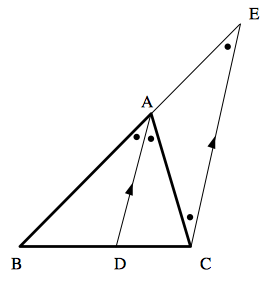$AD // EC$ なので， $$\color{red}{\underline{\color{black}{\angle BAD}}}=\color{blue}{\underline{\color{black}{\angle AEC}}} (\text{同位角})$$ $$\color{green}{\underline{\color{black}{\angle DAC}}}=\color{orange}{\underline{\color{black}{\angle ACE}}} (\text{錯角})$$ 仮定より，$\color{red}{\underline{\color{black}{\angle BAD}}}=\color{green}{\underline{\color{black}{\angle DAC}}}$ なので， $$\color{blue}{\underline{\color{black}{\angle AEC}}}=\color{orange}{\underline{\color{black}{\angle ACE}}}$$ よって，$△ACE$ は $AE=AC \cdots ①$ である二等辺三角形となる．
ここで，$△BCE$ において，$AD // EC$ より， $$BD:DC=BA:AE \cdots ②$$ である．①，②より， $$AB:AC=BD:DC$$ が成り立つ．
内角の二等分線の性質と同様に，つぎの外角の二等分線の性質も基本的です．
三角形の外角の二等分線と比： $AB\neq AC$ である $△ ABC$ の $\angle A$ の外角の二等分線と辺 $BC$ の延長との交点を $D$ とする．このとき，次の関係式が成り立つ． $$\large AB:AC=BD:DC$$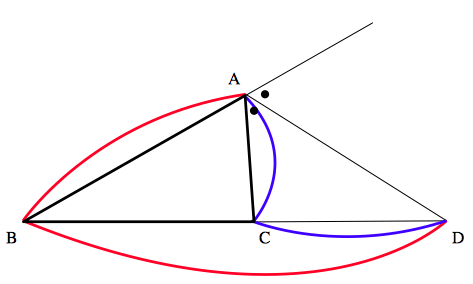 
証明： 一般性を失わずに，$AB > AC$ としてよい．点 $C$ を通り直線 $AD$ に平行な直線と，辺 $BA$ との交点を $E$ とする．また，下図のように，線分 $BA$ の ($A$ 側の) 延長上の点を $F$ とする．
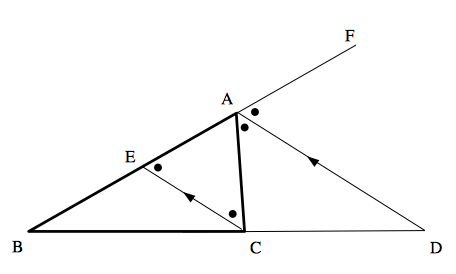$AD // EC$ なので， $$\color{red}{\underline{\color{black}{\angle FAD}}}=\color{blue}{\underline{\color{black}{\angle AEC}}} (\text{同位角})$$ $$\color{green}{\underline{\color{black}{\angle DAC}}}=\color{orange}{\underline{\color{black}{\angle ACE}}} (\text{錯角})$$ 仮定より，$\color{red}{\underline{\color{black}{\angle FAD}}}=\color{green}{\underline{\color{black}{\angle DAC}}}$ なので， $$\color{blue}{\underline{\color{black}{\angle AEC}}}=\color{orange}{\underline{\color{black}{\angle ACE}}}$$ よって，$△ACE$ は $AE=AC \cdots ①$ である二等辺三角形となる．
ここで，$△ABD$ において，$AD // EC$ より， $$BD:DC=BA:AE \cdots ②$$ である．①，②より， $$AB:AC=BD:DC$$ が成り立つ．
内角，外角の二等分線の性質は，その逆の命題も成り立ちます．
二等分線の性質の逆： $△ABC$ と直線 $BC$ 上の点 $D$ において，$AB:AC=BD:DC$ が成り立つならば，直線 $AD$ は $\angle A$ の二等分線である．
前節の二つの命題はおおざっぱに言えば，『三角形と角の二等分線が与えられたとき，ある辺の比の関係式が成り立つ．』というものでした．それに対して，上の命題は，『三角形とそのひとつの辺 (またはその延長) 上の点が与えられたとき，ある辺の比の関係式が成り立つならば，角の二等分線が隠れている．』という主張になります． 上の命題の証明は，前節のふたつの命題の証明を逆にたどれば示せます．
応用例として，別記事→アポロニウスの円で，この命題を用いています．
ここからはややマニアックな内容です．実は，角の二等分線の長さを，三角形の辺の長さなどで表すことができます．
内角の二等分線の長さ： $△ ABC$ の $\angle A$ の内角の二等分線と辺 $BC$ との交点を $D$ とする．このとき， $$\large AD^2=AB\times AC-BD\times DC$$ が成り立つ．
証明： $△ABC$ の外接円と，直線 $AD$ との交点のうち，$A$ でない方を $E$ とする．
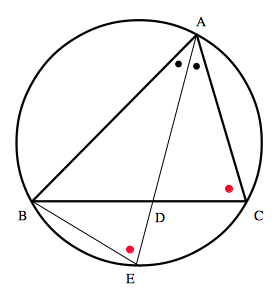
仮定より， $$\angle BAE=\angle CAD \cdots ①$$ 円周角の定理より， $$\angle BEA=\angle DCA \cdots ②$$ ①，②より，$△ABE \sim △ADC$ である．よって， $$AB:AE=AD:AC$$ したがって， $$AB\cdot AC=AD\cdot AE=AD(AD+DE)=AD^2+AD\cdot AE$$ また，方べきの定理より， $$AD\cdot AE=BD\cdot DC$$ よって， $$AD^2+AD\cdot AE=AD^2+BD\cdot DC$$ 以上より， $$AD^2=AB\times AC-BD\times DC$$ が成り立つ．
外角の二等分線の長さ： $△ ABC$ の $\angle A$ の外角の二等分線と辺 $BC$ の延長との交点を $D$ とする．このとき， $$\large AD^2=BD\times DC-AB\times AC$$ が成り立つ．
証明： 一般性を失うことなく，$AB>AC$ としてよい．$△ABC$ の外接円と，直線 $AD$ との交点のうち，$A$ でない方を $E$ とする．また，下図のように，直線 $AB$ の延長上の点を $F$ とする．
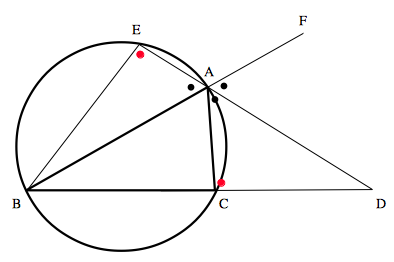
仮定より， $$\angle CAD=\angle DAF \cdots ①$$ また， $$\angle DAF=\angle BAE (\text{対頂角}) \cdots ②$$ さらに，円に内接する四角形の性質より， $$\angle BAE=\angle DAC \cdots ③$$ ②，③より，$△ABE \sim △ADC$ である．よって， $$AB:AE=AD:AC$$ したがって， $$AB\cdot AC=AD\cdot AE=AD(DE-AD)=AD\cdot DE-AD^2$$ また，方べきの定理より， $$AD\cdot DE=BD\cdot DC$$ よって， $$AB\cdot AC=BD\cdot DC-AD^2$$ 以上より， $$AD^2=BD\times DC-AB\times AC$$ が成り立つ．
