円と角度に関する基本的な定理である円周角の定理について解説します．
円周角の定理： $1$ つの弧に対する円周角の大きさは一定であり，その弧に対する中心角の大きさの半分である．
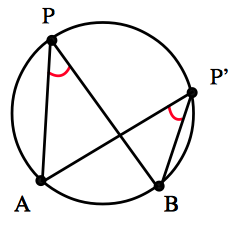
円周角の定理は，円に関する非常に基本的な定理です．まず，定理の前半部分の『$1$ つの弧に対する円周角の大きさは一定』とは，$4$ 点 $A,B,P,P’$ が下図のように同一円周上にあるとき，$\angle APB=\angle AP’B$ が成り立つということです．
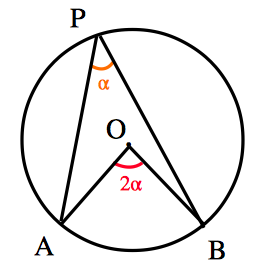
また，定理の後半部分の『円周角はその弧に対する中心角の半分』とは，下図において，$\angle APB=\frac{1}{2}\angle AOB$ が成り立つということです．
どちらも基本的で重要な事実です．
証明： $O$ を中心とする円上に $3$ 点 $A,P,B$ がある状況を考える．
Case1: 円の中心 $O$ が $\angle APB$ の内部にあるとき
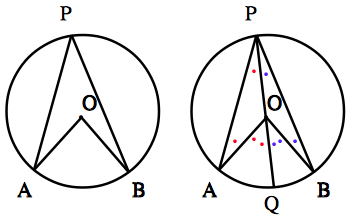直線 $PO$ と円との交点を $Q$ とする．$OP=OA$ より，$\angle APO=\angle PAO$.三角形の内角と外角の関係から，$\angle APO+\angle PAO=\angle AOQ.$ したがって，$\angle APO=\frac{1}{2}\angle AOQ.$ 同様にして，$\angle BPO=\frac{1}{2}\angle BOQ$. このふたつを合わせると， $$\angle APB=\frac{1}{2}\angle AOB$$ となる．
Case2: 円の中心 $O$ が線分 $PB$ 上にあるとき
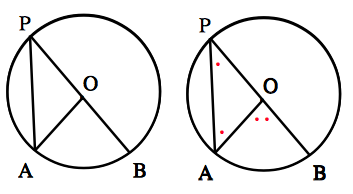$OP=OA$ より，$\angle APO=\angle PAO$.三角形の内角と外角の関係から，$\angle APO+\angle PAO=\angle AOB.$ したがって， $$\angle APB=\frac{1}{2}\angle AOB$$ となる．また，$O$ が線分 $AP$ 上にあるときも同じである．
Case3: 円の中心 $O$ が $\angle APB$ の外部にあるとき
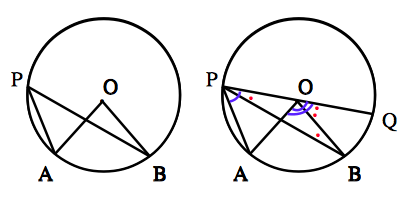直線 $PO$ と円との交点を $Q$ とする．$OP=OB$ より，$\angle OPB=\angle OBP.$ 三角形の内角と外角の関係から，$\angle OPB+\angle OBP=\angle BOQ.$したがって，$\angle BPO=\frac{1}{2}\angle BOQ.$ また，上のCase2 で証明した事実より，$\angle APO=\frac{1}{2}\angle AOQ$.これらを合わせると， $$\angle APB=\frac{1}{2}\angle AOB$$ となる．以上Case1〜3より，円周角は対応する中心角の半分であることが証明できた．
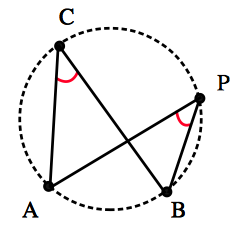
円周角の定理の逆： $2$ 点 $C,P$ が直線 $AB$ について，同じ側にあるとき，$\angle APB=\angle ACB$ ならば，$4$ 点 $A,B,C,P$ は同一円周上にある．
円周角の定理は，その逆の主張も成立します．これは，平面上の $4$ 点が同一周上にあるための判定法のひとつになっています．
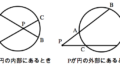
証明は次の事実により従います． 一つの円周上に $3$ 点 $A,B,C$ があるとき，直線 $AB$ について，点 $C$ と同じ側に点 $P$ をとるとき，$P$ の位置として次の $3$ つの場合がありえます． $1.$ $P$ が円の内部にある $2.$ $P$ が円周上にある $3.$ $P$ が円の外部にある
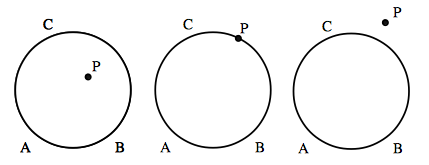
このとき，実は次の事実が成り立ちます． $1.$ $P$ が円の内部にある ⇔ $\angle APB > \angle ACB$ $2.$ $P$ が円周上にある ⇔ $\angle APB =\angle ACB$
$3.$ $P$ が円の外部にある ⇔ $\angle APB
したがって，$\angle APB =\angle ACB$ であることは，$P$ が円周上にあることと同値なので，これにより円周角の定理の逆が従います．
