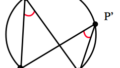
方べきの定理とは,円と線分の長さに関する定理です.この定理は大きくわけて $3$ つのシチュエーションで利用されます.
方べきの定理(1): 点 $P$ を通る $2$ 直線が,与えられた円と $2$ 点 $A,B$ および,$2$ 点 $C,D$ で交わるとき,次の等式が成り立つ. $$\large PA\times PB=PC\times PD$$
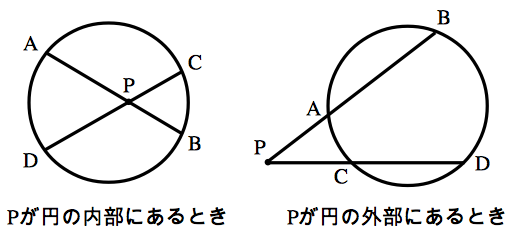
上図のように,方べきの定理(1) は点 $P$ が円の内部にある場合と,円の外部にある場合のふたつの状況が考えられます.どちらの状況についても, $$PA\times PB=PC\times PD$$ という線分の長さの関係が成り立っているのです.
方べきの定理(2): 円の外部の点 $P$ から円に引いた接線の接点を $T$ とする.$P$ を通り,この円と $2$ 点 $A,B$ で交わる直線をひくとき,次の等式が成り立つ. $$\large PA\times PB=PT^2$$
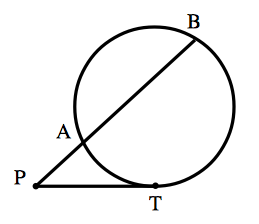
方べきの定理(2) は,右図のように,直線のひとつが円と接していて,もうひとつが円と $2$ 点で交わっているという状況です.これは方べきの定理(1) の特別な場合として考えることもできます.
この状況で, $$\large PA\times PB=PT^2$$ という線分の長さの関係式が成り立っているのです.
これらふたつを合わせて方べきの定理と呼びます.
証明のポイントは,円周角の定理や,円に内接する四角形の性質などを使い,$2$ つの三角形が相似であることを示し,その相似比を考えることです.
(1) の証明: $△PAC$ と $△PDB$ において,$P$ が円の内部にある場合は,円周角の定理により,また,$P$ が円の外部にある場合は,円に内接する四角形の性質により, $$\angle ACP=\angle DBP$$ $$\angle CAP=\angle BDP$$ 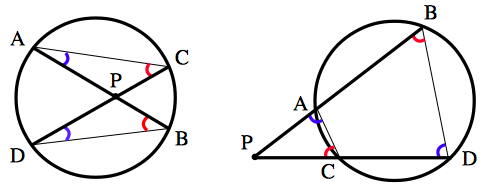 これらより, $△PAC$ と $△PDB$ は相似です. したがって, $PA:PD=PC:PB$ なので, $$PA\times PB=PC\times PD$$ です.
これらより, $△PAC$ と $△PDB$ は相似です. したがって, $PA:PD=PC:PB$ なので, $$PA\times PB=PC\times PD$$ です.
(2) の証明: $△PTA$ と $△PBT$ において,直線 $PT$ は円の接線なので,接弦定理より, $$\angle PTA=\angle PBT$$ また, $$\angle APT=\angle TPB$$ 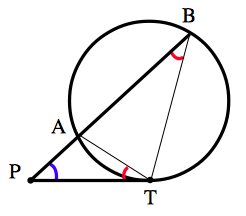
これらより, $△PTA$ と $△PBT$ は相似です. したがって, $PT:PB=PA:PT$
なので, $$PA\times PB=PT^2$$ です.
方べきの定理はそれぞれ次のように,その逆の主張も成り立ちます.
方べきの定理の逆: (1): $2$ つの線分 $AB,CD$ または,$AB$ の延長と $CD$ の延長が点 $P$ で交わるとき,$PA\times PB=PC\times PD$ が成り立つならば,$4$ 点 $A,B,C,D$ は同一円周上にある.
(2): 一直線上にない $3$ 点 $A,B,T$ と,線分 $AB$ の延長上の点 $P$ について,$PA\times PB=PT^2$ が成り立つならば,$PT$ は $3$ 点 $A,B,T$ を通る円に接する.
言葉で書くと少し主張がややこしく感じられますが,図で理解すると簡単です. (1) は,下図のような $2$ つの状況(のいずれか)について,
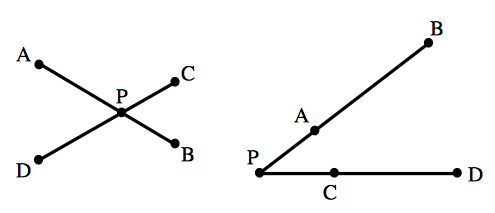
$$PA\times PB=PC\times PD$$ という等式が成り立っていれば,$4$ 点 $A,B,C,D$ は同一円周上にあるということです. (2)も同様で,下図のような状況について,
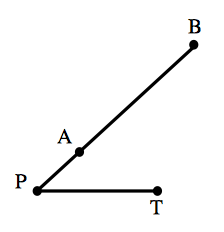
$$PA\times PB=PT^2$$ が成り立っていれば,$PT$ が $3$ 点 $A,B,T$ を通る円に接するということです. したがって,(1) はある $4$ 点が同一円周上にあることを示したいときに使え,(2) はある直線がある円に接していることを示したいときに使えます.
方べきの定理の逆は,方べきの定理を用いて証明することができます.
方べきの定理の逆の証明: (1) $2$ つの線分 $AB,CD$ が点 $P$ で交わるとき
$△ABC$ の外接円と,半直線 $PD$ との交点を $D’$ とすると,方べきの定理より, $$PA\times PB=PC\times PD’$$ 一方,仮定より, $$PA\times PB=PC\times PD$$ これらより,$PD=PD’$ となる.$D,D’$ はともに半直線PD上にあるので,点 $D$ と点 $D’$ は一致します.よって,$4$ 点 $A,B,C,D$ はひとつの円周上にあります. (2) 点 $A$ を通り,直線 $PT$ に $T$ で接する円と,直線 $PA$ との交点のうち $A$ でない方を $B’$ とする. 方べきの定理より, $$PA\times PB’=PT^2$$ 一方仮定より, $$PA\times PB=PT^2$$ これらより,$PB=PB’$ となる.
$B,B’$ はともに直線 $PA$ 上にあるので,点 $B$ と $B’$ は一致します.よって,$PT$ は $3$ 点 $A,B,T$ を通る円に接します.
問 下図において,$x,y$ の値はいくらか.
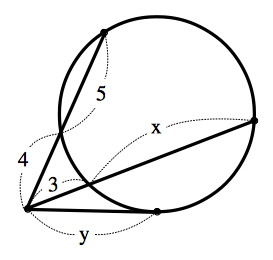
方べきの定理から, $$y^2=4\times 9=36$$ したがって,$y=6$ です.さらに方べきの定理より, $$36=3(x+3)$$ これを解くと,$x=9$ です.
問 $2$ つの円が $2$ 点 $Q,R$ で交わっている.線分 $QR$ 上に点 $P$ をとり,$P$ で交わる $2$ つの円の弦をそれぞれ,$AB,CD$ とする.このとき,$4$ 点 $A,B,C,D$ は同一円周上にあることを示せ.
方べきの定理を二度用いると, $$PA\times PB=PQ\times PR$$ $$PC\times PD=PQ\times PR$$ です.これら二式より, $$PA\times PB=PC\times PD$$ よって,方べきの定理の逆より,$4$ 点 $A,B,C,D$ は同一円周上にあります.