アポロニウスの円とは何か，またその中心と半径について紹介します．
平面上に，$2$ 点 $A,B$ が与えられたとき，$A,B$ からの距離の比が $1:1$ であるような点の軌跡は線分 $AB$ の垂直二等分線になります．
では，$A,B$ からの距離の比が $m:n$ (ただし，$m \neq n$) であるような点の軌跡はどのようになるでしょうか．実は，次の美しい定理が成り立ちます．
定理： $m,n$ を相異なる正の実数とする．平面上の $2$ 点 $A,B$ からの距離の比が $m:n$ であるような点の軌跡は円である．
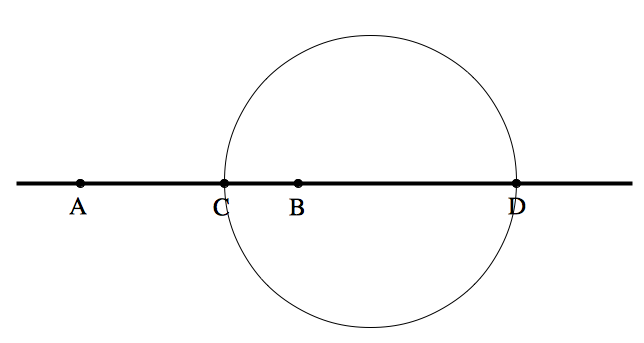
この円のことをアポロニウスの円と言います．たとえば，下図の円は $A,B$ からの距離の比が $2:1$ であるような点の軌跡を表しています．つまり，この円上のどの点 $P$ に対しても，$AP:BP=2:1$ が成り立ちます．
上の定理が成り立つことは，簡単な初等幾何学の知識で示すことができます．
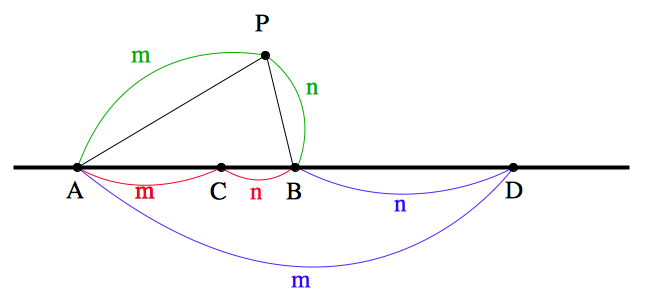
証明： 直線 $AB$ 上において，線分 $AB$ を $m:n$ に内分,外分する点をそれぞれ $C,D$ とする．また，点 $P$ を $AP:BP=m:n$ を満たし，直線 $AB$ 上にない点とする．
角の二等分線の性質より，直線 $PC,PD$ はそれぞれ $\angle APB$ の内角，外角の二等分線である．
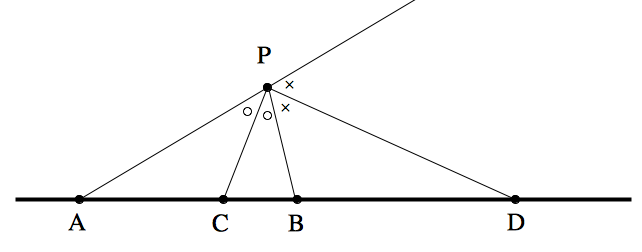
したがって，$\angle CPD=90°$ である．
よって，点 $P$ は線分 $CD$ を直径とする円周上の点である．ゆえに点 $P$ の軌跡は円となる．
ここからは少しマニアックな内容になりますが，アポロニウスの円の中心がどのような位置にあるか考えてみましょう．実は次の美しい事実が成り立ちます．
アポロニウスの円の中心： $m,n$ を相異なる正の実数とする．平面上の $2$ 点 $A,B$ からの距離の比が $m:n$ であるような点の軌跡は円である．この円の中心は線分 $AB$ を $m^2:n^2$ に外分する点である．
証明： 直線 $AB$ 上において，線分 $AB$ を $m:n$ に内分,外分する点をそれぞれ $C,D$ とする．$A(x_1,y_1)，B(x_2,y_2)$ とおく．
点 $C$ は線分 $AB$ を $m:n$ に内分するので， $$C \left(\frac{nx_1+mx_2}{m+n}, \frac{ny_1+my_2}{m+n}\right)$$ である．同様に，点 $D$ は線分 $AB$ を $m:n$ に外分するので， $$D \left(\frac{-nx_1+mx_2}{m-n}, \frac{-ny_1+my_2}{m+n}\right)$$ である．アポロニウスの円の中心は線分 $CD$ の中点にあるから，その $x$ 座標は， $$\frac{1}{2}\left(\frac{nx_1+mx_2}{m+n}+\frac{-nx_1+mx_2}{m-n}\right)$$ $$=\frac{1}{2}\left(\frac{(m-n)(nx_1+mx_2)+(m+n)(-nx_1+mx_2)}{m^2-n^2}\right)$$ $$=\frac{-n^2x_1+m^2x_2}{m^2-n^2}$$ となる．$y$ 座標も同様にして， $$\frac{1}{2}\left(\frac{ny_1+my_2}{m+n}+\frac{-ny_1+my_2}{m-n}\right)$$ $$=\frac{1}{2}\left(\frac{(m-n)(ny_1+my_2)+(m+n)(-ny_1+my_2)}{m^2-n^2}\right)$$ $$=\frac{-n^2y_1+m^2y_2}{m^2-n^2}$$ となる．よって，アポロニウスの円の中心は，線分 $AB$ を $m^2:n^2$ に外分する点である．
ついでに，アポロニウスの円の半径も求めてみましょう．次の事実が成り立ちます．
アポロニウスの円の半径： $m,n$ を相異なる正の実数とする．平面上の $2$ 点 $A,B$ からの距離の比が $m:n$ であるような点の軌跡は円である．この円の中心を $O$ とするとき，この円の半径は $\sqrt{OA\times OB}$ である．
証明： 直線 $AB$ 上において，線分 $AB$ を $m:n$ に内分する点を $C$ とする．また，求める円の半径を $r$，線分 $AB$ の長さを $k$ とおく． 点 $C$ は線分 $AB$ を $m:n$ に内分するので， $$BC=\frac{n}{m+n}k$$ である．また，点 $O$ は線分 $AB$ を $m^2:n^2$ に外分する点であったから， $$OA=\frac{m^2}{m^2-n^2}k$$ である．したがって， $$OB=OA-AB=\frac{m^2}{m^2-n^2}k-k=\frac{n^2}{m^2-n^2}k$$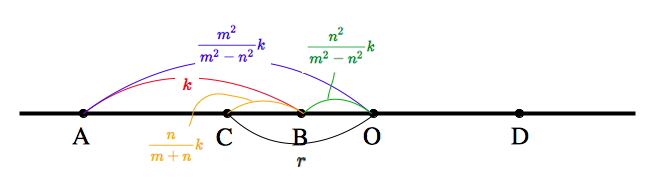 
以上より， $$r=OB+BC=\frac{n^2}{m^2-n^2}k+\frac{n}{m+n}k=\frac{mn}{m^2-n^2}k=\sqrt{OA\times OB}$$ よって，アポロニウスの円の半径は $\sqrt{OA\times OB}$ である．
