ホーム >> 三角比・三角関数 >> 余弦定理の証明と使いどころ
2016/7/11 
図形と計量
かなり重点的に問われることの多い余弦定理について解説します．
余弦定理とは，三角形の $3$ 辺とひとつの角の余弦に関する以下の関係式のことです．
余弦定理: $△ABC$ について，次の等式が成り立つ．
$$a^2=b^2+c^2-2bc\cos A,\ \ \cos A=\frac{b^2+c^2-a^2}{2bc}$$ $$b^2=c^2+a^2-2ca\cos B,\ \ \cos B=\frac{c^2+a^2-b^2}{2ca}$$ $$c^2=a^2+b^2-2ab\cos C,\ \ \cos C=\frac{a^2+b^2-c^2}{2ab}$$
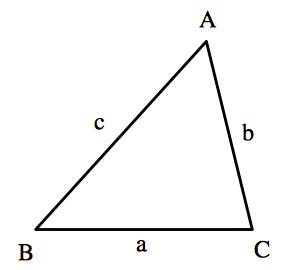ここで，$△ABC$ の $3$ 辺 $a,b,c$ はいつものように右の図のような位置関係にある辺です．左右に並べられた $2$ つの等式は式変形すれば同じものですが，どちらの形もよく使うので，$2$ 種類とも並べました．
ひとつの角 (たとえば $A$ ) が $90°$ のとき，$\cos A=0$ なので，これを余弦定理に代入すれば，$a^2=b^2+c^2$ が成り立ちます．これは三平方の定理に他なりません．この意味で，余弦定理は三平方の定理の一般化と考えることができます．
最も簡単な証明方法はベクトルを用いる方法です．
証明: $$a^2=|\vec{a}|^2=\left|\overrightarrow{BC}\right|^2=\left|\overrightarrow{AC}+\overrightarrow{BA}\right|^2$$ $$=\left|\overrightarrow{AC}\right|^2 +\left|\overrightarrow{BA}\right|^2+2 \cdot \overrightarrow{AC} \cdot \overrightarrow{BA}$$ $$=\left|\overrightarrow{AC}\right|^2 +\left|\overrightarrow{BA}\right|^2-2 \cdot \overrightarrow{AC} \cdot \overrightarrow{AB}$$ $$=b^2+c^2-2bc\cos \angle A$$ その他の公式も同様にして導かれる．
また，座標を導入して求めることもできます．
証明: 上の図において，$B(c,0),C(b\cos A,b\sin A)$ より， $$BC^2=(b\cos A-c)^2+(b\sin A)^2=b^2+c^2-2bc\cos A$$ 一方，$BC=a$ なので， $$a^2=b^2+c^2-2bc\cos A$$ となる．その他の公式も同様にして導かれる．
冒頭で述べたように，重要なことは，余弦定理は，三角形の $3$ 辺とひとつの角に関する関係式であるということです．この $3$ 辺と $1$ 角の合計 $4$ つの情報のうち，$3$ つがわかっていれば，余弦定理によって，$4$ つ目の情報を手に入れることができるのです．したがって，余弦定理の使い方は主に $2$ パターンあります．
Patern $1$:三角形の $3$ 辺が与えられたとき
たとえば，上の図のように三角形の $3$ 辺の長さがわかっているとき，三角形の内角の余弦がわかります． $$\cos A=\frac{2^2+(1+\sqrt{3})^2-(\sqrt{6})^2}{2\cdot2\cdot(1+\sqrt{3})}=\frac{1}{2}$$ したがって，$A=60°$ です．
Patern $2$:三角形の $2$ 辺と $1$ 角が与えられたとき
今度は上の図のように三角形の $2$ 辺と $1$ 角がわかっているとき，三角形のもうひとつの辺がわかります． $$(\sqrt{2})^2=2^2+a^2-4a\cos 30°$$ より，$2=4+a^2-2\sqrt{3}a$ となって，これを整理すると，$a^2-\sqrt{3}a+2=0$ となります． これを解くと，$$a=\sqrt{3}+1,\sqrt{3}-1$$ 答えが $2$ つ表れました．実は，$AB=2,AC=\sqrt{2},\angle BAC=30°$ を満たす三角形は下の図のよに $2$ 種類あります．
