整数分野の中でも,わかりにくいけれど非常に重要な概念である互いに素について解説します.
$2$ つの整数 $a,b$ について,どちらの約数でもある数を $a,b$ の公約数と言います.たとえば,$(4,8)$ の公約数は $1,2,4$ です.約数として,負の数を考えることもありますが,一般には正の数のみを考えることが多いので,単に約数といえば (正の約数) のことを言っていると理解してください.公約数のうち,最大のものを最大公約数と呼びます.上の例でいえば,最大公約数は $4$ です.
さて,$2$ つの整数 $a,b$ が互いに素とは,公約数が $1$ のみであることを言います.これは,最大公約数が $1$ であることと同値です.
たとえば,$(2,3)$ や $(8,21)$ や $(1,5)$ などは互いに素です. 一方,$(2,6)$ や $(4,14)$ などは互いに素ではありません.
特に,$1$ と全ての数は互いに素です.
互いに素というのは言い換えれば,共通の素因数を持たないということです.たとえば,$8$ の素因数は $2$ で,$21$ の素因数は $3,7$ です.したがって,$8$ と $21$ は共通の素因数を持っていないので,互いに素です.
このように考えると,互いに素という言葉は否定的な意味合いを含む否定語だと思えます.したがって,証明などで扱うときは,その否定を考えて肯定語に直したほうが扱いやすい場合が多いです.次の問の証明が良い例です.
問 $m$ を整数とする.$m$ と $m+1$ は互いに素であることを示せ.
この事実は基本的ですが非常に重要なので,覚えておいたほうが良いでしょう.証明は次のようにすればよいです.
証明 $m$ と $m+1$ が互いに素でないと仮定する(背理法).このとき,$m$ と $m+1$ は共通の素因数 $d$ を持ち,整数 $a,b$ を用いて, $$m=ad, m+1=bd$$ とかける.すると, $$d(b-a)=1$$ となるが,$d,b-a$ はともに整数なので,$d$ が $1$ の約数であることになり矛盾. よって,$m$ と $m+1$ は互いに素である.
このように互いに素の否定を考えれば,大抵の証明問題はうまくいきます.
整数分野で非常に重要な事実として,次のようなものがあります.証明を理解するよりは,この主張の意味を理解することが大切です.
次の $2$ つの条件は同値 ($1$) $m$ と $n$ が互いに素である.
($2$) $x,y$ の不定方程式 $mx+ny=1$ が整数解をもつ.
証明 まず,($2$) ⇒ ($1$) を示す.対偶が成り立つことを示せばよい.$m$ と $n$ が互いに素でないとすると,$m$ と $n$ は共通の素因数 $d$ を持ち,整数 $a,b$ を用いて, $$m=ad,n=bd$$ とかける.すると,$mx+ny=d(ax+by)$ となり,これが整数解をもつとすると,$d$ が $1$ の約数となり矛盾するので,整数解はもたない. つぎに,($1$) ⇒ ($2$) を示す.整数 $x,y$ を用いて,$mx+ny$ と表せる数全体の集合を $M$ とおく.$M$ に属する正の整数のうち,最小のものを $d$ とおく.すると,$M$ の元はすべて $d$ の倍数となる.以下,それを示す.$d \in M$ より,整数 $x_0,y_0$ を用いて,$d=mx_0+ny_0$ とかける.いま,$M$ の任意の元 $mx+ny$ を $d$ で割ったときの商を $q$,余りを $r$ とすると, $$mx+ny=dq+r (0 \le r < d)$$ となる.したがって, $$r=mx+ny-dq=m(x-x_0q)+n(y-y_0q)$$ よって,$r \in M$ となる.もし,$r >0$ なら,$d$ の最小性に反するので,$r=0$ でなければならない.よって,$M$ の元はすべて $d$ の倍数となる.
さて,$m,n \in M$ であるから,$d$ は $m$ と $n$ の約数であるが,$m,n$ は互いに素なので,$d=1$ となる.したがって,$1 \in M$ .これは,$x,y$ の不定方程式 $mx+ny=1$ が整数解をもつことを意味している.
つまり,不定方程式 $mx+ny=1$ が整数解をもつかどうかは,$x$ と $y$ の係数 $m,n$ を見ればひと目でわかるということです.以下,このことを用いて,互いに素の意味に迫りたいと思います.
さて,$2$ つの整数が互いに素というのはどのように意味づけることができるでしょうか.ここで,上で見た互いに素と同値な条件について考えてみましょう.『$x,y$ の不定方程式 $mx+ny=1$ が整数解をもつ.』とは,次のような意味だと考えるとわかりやすいです. 数直線上の原点 $X$ に一匹のバッタが止まっている状況を考えてみてください.このバッタは $2$ 種類のジャンプができます.現在の地点からちょうど $m$ 離れた場所にジャンプするか,あるいはちょうど $n$ 離れた場所にジャンプするかのいずれかです.
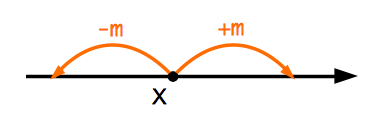
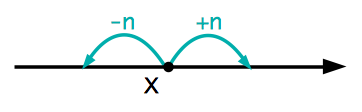
『$x,y$ の不定方程式 $mx+ny=1$ が整数解をもつ.』というのは,『バッタが原点からこの $2$ 種類のジャンプを何回か行って,結果的に $1$ だけ進むことができる』ということに対応しています.もし,バッタが原点から $1$ だけ進むことが可能ならば,数直線上の整数点すべてにとまることが可能です.要するに,$m$ と $n$ が互いに素というのはバッタのジャンプ幅が絶妙にずれている様子を表しているのです.

