組合せの最も基本的な事柄と,よくある組合せの問題を解説します.
いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています.
順列 $\rightarrow$ 順序を考慮 (区別)する.
組合せ $\rightarrow$ 順序を考慮 (区別)しない.
たとえば,$A,B,C,D$ という $4$ 種類の記号があるとき,これらから異なる $2$ つを取り出して,並べる順序を考慮せず,$2$ つの組をつくる方法は,下のように $6$ 通りあります. \begin{array}{ccc} \{A,B\}&\{A,C\}&\{A,D\}\\ \{B,C\}&\{B,D\}&\{C,D\} \end{array} つまり組合せの問題では,どう並べるかは全く問題ではなく,何を取りだしたかだけが問題でなのです.
一般に,異なる $n$ 個のものから異なる $r$ 個を取り出してつくる組合せの総数を $\color{red}{{}_n \mathrm{C} _r}$ という記号で表します.(読み方は,コンビネーションエヌアール,またはエヌシーアールなど) ${}_n \mathrm{C} _r$ は非常に重要な数で,二項係数と呼ばれます.
上の例より,${}_4 \mathrm{C} _2=6$ であることがわかります. さて,一般の ${}_n \mathrm{C} _r$ はどのような値となるのでしょうか.
${}_n \mathrm{C} _r$ を計算するために,まず,異なる $n$ 個のものから異なる $r$ 個を取り出して並べる順列を考えます.この総数は, $${}_n \mathrm{P} _r=n(n-1)(n-2)\cdots (n-r+1)$$ であることは,順列の記事で紹介しました.これらの順列のうち,組合せとして同じものがどれだけあるか考えます.異なる $r$ 個のものを一列にならべる順列の総数は $r!$ 通りです.実は,これら $r!$ 個の順列がちょうどひとつの組合せに対応しています.たとえば,下図は $n=4,r=3$ の場合です.この例では,$3!=6$ 個の順列がひとつの組合せに対応しています.
したがって,一般に次の公式が成り立ちます. $${}_n \mathrm{C} _r=\frac{{}_n \mathrm{P} _r}{r!}=\frac{n(n-1)(n-2)\cdots (n-r+1)}{r!}$$ さらに,最右辺の式の分母分子に,$(n-r)!$ をかけると, $${}_n \mathrm{C} _r=\frac{n(n-1)(n-2)\cdots (n-r+1)\{(n-r)!\}}{r!(n-r)!}=\frac{n!}{r!(n-r)!}$$ となって,二項係数を階乗記号を用いてきれいに表すことができます.この公式は非常に基本的で重要です.
組合せの総数: 異なる $n$ 個のものから異なる $r$ 個のものを取り出す組合せの総数は $\large {}_n \mathrm{C} _r=\frac{n!}{r!(n-r)!}$
具体的な問題を通して,組合せの考え方に慣れましょう.
例題 男子 $5$ 人女子 $4$ 人から,男子 $2$ 人,女子 $2$ 人の委員を選ぶ方法は何通りあるか.
人は当然区別がつくものと考えます.まず,男子 $5$ 人から $2$ 人を選ぶ方法は,${}_5 \mathrm{C} _2=10$ 通りです.(選ぶだけなので,順列ではなく組合せの問題です) また,女子 $4$ 人から $2$ 人を選ぶ方法は,${}_4 \mathrm{C} _2=6$ 通りです.したがって,積の法則より,求めるべき場合の数は $10\times 6=60$ 通りです.
例題 正六角形の対角線は何本あるか.
正六角形の頂点から,異なる $2$ つを選ぶ方法は,${}_6 \mathrm{C} _2=15$ 通りです.つまり,正六角形の相異なる $2$ 頂点を結んでできる辺の総数は $15$ 本です.このうち,正六角形の辺であるものが $6$ 通り存在します.したがって,対角線の本数は $15-6=9$ 通りです.
例題 下図のような格子状の街路がある.地点 $A$ から地点 $B$ まで最短の経路で行く方法は何通りあるか.
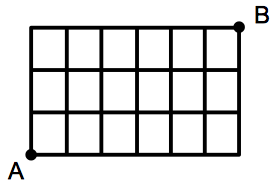
このような最短経路の問題もよくみられます.次のように考えます.$A$ から $B$ まで最短で行くには,ちょうど上に $3$ マス,右に $6$ マス進まなければなりません.上に $1$ マスいくことを $\uparrow$ で表し,右に $1$ マスいくことを $\rightarrow$ で表すことにします.すると,$A$ から $B$ までの行き方は,$3$ つの $\uparrow$ と $6$ つの $\rightarrow$ を一列に並べる方法の総数に一致します.たとえば,下図において,左図の行き方は右図の並べ方に対応しています.要するに,矢印の順列の左から順にしたがって進んでいくと,それが $A$ から $B$ までの最短経路のひとつになっているのです.
さてここで,下図のように $9$ つのマスを用意します.
この $9$ つのマスから $3$ つのマスを選ぶ方法は,${}_9 \mathrm{C} _3=84$ 通りあります.選んだ $3$ つのマスに $\uparrow$ をいれて,残りのマスに $\rightarrow $ を入れれば,これは $A$ から $B$ までのひとつの行き方に対応しています.
以上より,$A$ から $B$ までの最短経路の本数は $84$ 通りです.
問 $8$ 人の生徒のうち,$4$ 人を選びそのうちのひとりを代表とする決め方は何通りあるか.
まず,$8$ 人から $4$ 人を選ぶ方法は ${}_8 \mathrm{C} _4=70$ 通り.そのそれぞれの選び方に対して,代表の決め方が $4$ 通りある.したがって,$70\times 4=280$ 通り.
先に代表を決めてから残りの $3$ 人を選ぶという考え方でも解ける.この場合,代表の決め方は $8$ 通り.その各々に対して,代表以外の $7$ 人から $3$ 人を選ぶ方法は,${}_7 \mathrm{C} _3=35$ 通り.したがって,$8\times 35=280$ 通り.当然答えは上のものと同じになる.
問 正八角形の頂点のうち,相異なる $3$ 点を頂点とする二等辺三角形は何通りあるか.
正八角形の頂点のうち,相異なる $3$ 点を頂点とする二等辺三角形は,形のみに着目すると次の $3$ 種類しかない.(言い換えれば,二等辺三角形の頂点が一番上にくるとした場合は下図の $3$ 通りしかない.)
それぞれ $8$ 通りあるので,$3\times 8=24$ 通り.
問 下図のような格子状の街路がある.地点 $A$ から地点 $B$ まで,地点 $P$ を通らずに最短の経路で行く方法は何通りあるか.
地点 $A$ から地点 $B$ まで何の制約もなく行く方法は ${}_9 \mathrm{C} _3=84$ 通り.また,地点 $A$ から地点 $P$ まで行く方法は ${}_4 \mathrm{C} _1=4$ 通り.さらに,地点 $P$ から地点 $B$ まで行く方法は ${}_5 \mathrm{C} _2=10$ 通り.
したがって,地点 $A$ から地点 $P$ を通って地点 $B$ まで行く方法は,$4\times 10=40$ 通り.よって,求めるべき場合の数は $84-40=44$ 通り.
