$1$ 点の座標と直線の式が与えられたとき,その点と直線との距離を求める公式を導出します.この公式は非常に重要で便利である上に,式がきれいなので覚えやすいです.
座標平面上に,$1$ 点 $A$ と直線 $l$ が与えられているとします.
$A$ から直線 $l$ に垂線をおろし,その足を $H$ とします.
$1$ 点 $A$ と直線 $l$ との距離とは,$AH$ の長さのことです.
これは,点 $P$ が直線 $l$ 上を動くときの $AP$ の長さの最小値でもあります.
まずは,直線の式が $y=mx+n$ という形で与えられている場合を考えてみましょう.
点と直線の距離の公式1: $1$ 点 $(x_1,y_1)$ と直線 $y=mx+n$ の距離を $d$ とすると,次が成り立つ. $$\large d = \frac{|y_1-mx_1-n|}{\sqrt{1+m^2}}$$
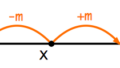
この公式は次のようにして,示すことができます.まず,下図のように,$1$ 点 $A(x_1,y_1)$ と直線 $l:y=mx+n$ があり,$A$ から直線 $l$ におろした垂線の足を $H$ としましょう.$AH=d$ です.
さらに,下図のように $2$ つの直角三角形を作ります.つまり,点 $C$ を $AC$ が $y$ 軸に平行で,$BC=m$ となるようにとり,$C$ を通り $x$ 軸に平行な直線と直線 $l$ との交点を $D$ とします.直線 $l$ の傾きは $m$ なので,$DC=1$ です.
また,$AB=|y_1-(mx_1+n)|=|y_1-mx_1-n|$ で,$DB=\sqrt{1+m^2}$ です.
さて,上図の $2$ つの直角三角形 $△ABH$ と $△DBC$ は相似なので, $$AB:AH=DB:DC$$ すなわち, $$|y_1-mx_1-n|:d=\sqrt{1+m^2}:1$$ したがって, $$d=\frac{|y_1-mx_1-n|}{\sqrt{1+m^2}}$$ となって,確かに公式が成り立ちます.
つぎは,直線の式が $ax+by+c=0$ という形で表されている場合です.この場合の公式のほうが使いやすいかもしれません.
点と直線の距離の公式2: $1$ 点 $(x_1,y_1)$ と直線 $ax+by+c=0$ の距離を $d$ とすると,次が成り立つ. $$\large d = \frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
これは,$y=mx+n$ 型の公式から容易に導かれます.
$b\neq 0$ のとき
直線の式 $$ax+by+c=0$$ を変形すると, $$y=-\frac{a}{b}x-\frac{c}{b}$$ となります.したがって,前節における公式に,$m=-\frac{a}{b},n=-\frac{c}{b}$ を代入すると,$1$ 点 $(x_1,y_1)$ と直線 $ax+by+c=0$ との距離 $d$ は, $$d=\frac{|y_1+\frac{a}{b}x_1+\frac{c}{b}|}{\sqrt{1+\left(-\frac{a}{b}\right)^2}}=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
$b=0$ のとき
直線の式は $ax+c=0$ すなわち,$x=-\frac{c}{a}$ となります.
これは,$y$ 軸に平行な直線なので,$1$ 点 $(x_1,y_1)$ と直線 $x=-\frac{c}{a}$ との距離 $d$ は, $$d=\left|x_1+\frac{c}{a}\right|=\frac{|ax_1+c|}{|a|}$$ これは,公式 $$d = \frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$ において,$b=0$ としたものに他なりません.
以上より,いずれの場合も上の公式が成り立つことが示されました.