平面図形の基本的な定理である中点連結定理とその逆について紹介します.
中点連結定理とは,三角形の2辺の中点同士を結んだ線分に関する定理です.具体的には次のような主張です.
中点連結定理: $△ABC$ について,辺 $AB,AC$ の中点をそれぞれ $M,N$ とするとき,次の2つが成り立つ. $$\large (i) MN\ // \ BC$$ $$\large (ii) MN=\frac{1}{2}BC$$
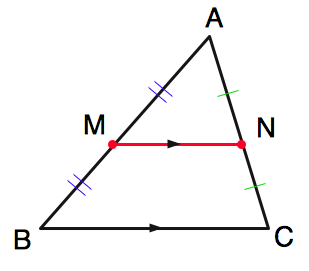
つまり,$△ABC$ について,$M$ を $AB$ の中点 (すなわち線分 $AB$ を二等分する点) ,$N$ を $AC$ の中点とすると,$MN$ と $BC$ は平行であって,さらに $MN$ の長さは $BC$ の半分である,ということです.
中点連結定理は三角形の相似を使って証明することができます.以下がその証明です.
証明: $△ABC$ と $△AMN$ について考えます. まず, $$\angle BAC = \angle MAN$$ が成り立ちます.つぎに, $$AB=2AM,AC=2AN$$ なので, $$AB:AM=AC:AN=2:1$$ です.よって,$△ABC$ と $△AMN$ は相似です.相似比が $2:1$ なので,$$MN=\frac{1}{2}BC$$ が成り立ちます.また,$\angle ABC =\angle AMN$ であり,同位角が等しいので,$$MN \ // \ BC$$ です.
中点連結定理はその逆も成り立ちます.中点連結定理の逆の主張は次のようになります.
中点連結定理の逆: $△ABC$ について,線分 $AB$ 上に点 $M$ をとり,線分 $AC$ 上に点 $N$ をとる.このとき,次の $(i),(ii)$ が成り立つならば,$M,N$ はそれぞれ $AB,AC$ の中点である.
$$\large (i) MN\ // \ BC$$ $$\large (ii) MN=\frac{1}{2}BC$$
証明: 先に仮定と結論を書いておきます.
仮定:$MN\ // \ BC,MN=\frac{1}{2}BC$
結論:$M$ は線分 $AB$ の中点,$N$ は線分 $AC$ の中点 まず,$M$ を通り,線分 $AC$ に平行な直線をひき,これと線分 $BC$ との交点を $L$ とします.
このとき,$MN\ //\ LC,ML\ //\ NC$ なので,四角形 $MLCN$ は平行四辺形です.
さて,$△AMN$ と $△MBL$ が合同であることを示しましょう.$MLCN$ は平行四辺形なので,$MN=LC$ です.一方,仮定より $MN=\frac{1}{2}BC$ なので,$L$ は線分 $BC$ の中点であることがわかります.よって $$MN=BL・・・(1)$$ です.また,$MN\ //\ BC$ より, $$\angle AMN=\angle MBL・・・(2)$$ さらに,$ML\ //\ AC$ より, $$\angle ANM=\angle MLB・・・(3)$$ $(1),(2),(3)$ より, $$△AMN \equiv △MBL$$ です.これより $AM=MB$ なので,$M$ は線分 $AB$ の中点です.また,$△AMN \equiv △MBL$ より $ML=AN$ ,$MLCN$ は平行四辺形なので,$ML=NC$ ですから,$N$ は線分 $AC$ の中点であることもわかります.
問 $△ABC$ について,$AB,BC,CA$ の中点をそれぞれ $P,Q,R$ とする.このとき $△PQR$ の周の長さは $△ABC$ の周の長さの何倍か.
問 $AB\ //\ CD$ である台形 $ABCD$ について,$AD$ の中点を $M$,$BC$ の中点を $N$ とすると,次が成り立つことを示せ. $$(i) MN \ //\ AB$$ $$(ii) MN=\frac{1}{2}(AB+CD)$$
$B$ を通り,$AD$ に平行な直線をひき,これと $CD$ との交点を $E$ とする.四角形 $ABED$ は平行四辺形である.$△BEC$ に中点連結定理を適用する.
問 四角形 $ABCD$ について,$AB,BC,CD,DA$ の中点をそれぞれ $O,P,Q,R$ とする.このとき,四角形 $OPQR$ は必ず平行四辺形となることを示せ.
四角形 $ABCD$ の対角線を一本ひき,それぞれの三角形について,中点連結定理を適用する.
