円に内接する四角形はメジャーですが,今回はそれよりもマイナーな,円に外接する四角形についてです.
どのような三角形も必ず内接円をもちます.つまり,三角形の $3$ 辺と接するような円が存在します.ところが,四角形の場合はそうではありません.内接円がある四角形もあれば,ない四角形も存在します.内接円がある四角形,すなわち $4$ 辺と接する円が存在する四角形は,円に外接するといいます.どのような四角形が円に外接するのでしょうか.
実は,四角形が円に外接するための必要十分条件は,$2$ 組の対辺の和が等しくなることです.
四角形 $ABCD$ が円に外接するための必要十分条件は, $$\large AB+CD=BC+DA$$
$AB+CD=BC+DA$ が,四角形 $ABCD$ が円に外接するための必要条件であることを示します.つまり,四角形 $ABCD$ が円に外接すると仮定して,$AB+CD=BC+DA$ を導きます.この証明は簡単です.
必要性の証明: 四角形 $ABCD$ が円に外接すると仮定する.線分 $AB,BC,CD,DA$ と円との接点をそれぞれ,$P,Q,R,S$ とすると, $$AP=AS,\ BP=BQ,\ CQ=CR,\ DR=DS$$ が成り立つ.したがって, $$AB+CD=(AP+BP)+(CR+DR)=(AS+BQ)+(CQ+DS)$$ $$=(BQ+CQ)+(AS+DS)=BC+DA$$
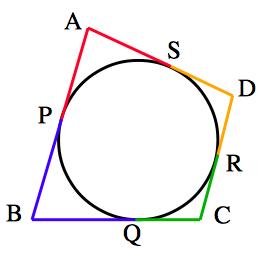
円の外の点から,円にひいた $2$ 本の接線の長さ (正確には点と接点との距離) は等しくなります.つまり,右図で同じ色の線分は同じ長さです.すると,対辺の和というのは,$4$ 色の線分をひとつづつ足したものになります.$2$ 組の対辺の和が等しいのは一目瞭然です.
つづいて,$AB+CD=BC+DA$ が,四角形 $ABCD$ が円に外接するための十分条件であることを示します.つまり,$AB+CD=BC+DA$ を満たす四角形 $ABCD$ はある円に外接することを示します.この証明を自力で思いつけたらかなり実力があると思います.
十分性の証明: まず,$AB,BC,CD,DA$ のうち,長さが最小の線分を $AB$ としておく.(このようにしても一般性は失われない)
Case1: $AB=BC$ のとき
この場合は,条件 $AB+CD=BC+DA$ から,$CD=DA$ となるので,四角形 $ABCD$ は凧形 (たこがた) になる.凧形の四角形は円に外接する.実際,$\angle BAD$ の二等分線と線分 $BD$ の交点を $O$ とすると,$O$ は各線分 $AB,BC,CD,DA$ から等距離にある点である.
証明つづき:
Case2: $AB < BC$ のとき $AB < BC$ より,線分 $BC$ 上に,$AB=BP$ となるような点 $P$ がとれる.さらに,線分 $CD$ 上に $CP=CQ$ となる点 $Q$ をとる.(このような点 $Q$ を線分 $CD$ 上にとるためには,$CQ < CD$ が成り立ってないといけないが,仮定から $AB+CD=BC+DA$ なので,$BC < AB+CD$ が成り立っている.これより,$CQ < CD$ が導かれる.) このとき,仮定から $2$ 組の対辺の和が等しいので,$AD=DQ$ となる.したがって,$△BAP,△CPQ,△DAQ$ はすべて二等辺三角形で,頂点 $B,C,D$ から線分 $AP,PQ,PA$ へ下ろした垂直二等分線は,$△APQ$ の外心 $O$ で交わる.すると,この外心 $O$ は線分 $AB,BC,CD,DA$ から等距離にある点である.
以上より,$AB+CD=BC+DA$ を満たす四角形 $ABCD$ はある円に外接する.
四角形が円に外接するための必要十分条件がこのような簡単な式で表せられるのは驚くべきことですね.
