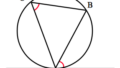
メネラウスの定理とは,三角形と,その頂点を通らないひとつの直線があるときに成り立つ線分の比に関する定理です.証明は平行線と比の定理を $2$ 回用いることにより示せます.
メネラウスの定理: $△ABC$ の辺 $BC,CA,AB$ またはそれらの延長が,三角形の頂点を通らない直線 $l$ とそれぞれ $P,Q,R$ で交わるとき,次の等式が成り立つ. $$\frac{BP}{PC}\frac{CQ}{QA}\frac{AR}{RB}=1$$
証明: $△ABC$ の頂点 $C$ を通り,直線 $l$ に平行な直線を引き,直線 $AB$ との交点を $D$ とする.平行線と比の定理より, $$BP:PC=BR:RD$$ すなわち, $$\frac{BP}{PC}=\frac{BR}{RD} \cdots (1)$$ 同様に, $$AQ:QC=AR:RD$$ より, $$\frac{CQ}{QA}=\frac{DR}{RA} \cdots(2)$$ $(1),(2)$ より, $$\frac{BP}{PC}\frac{CQ}{QA}\frac{AR}{RB}=\frac{BR}{RD}\frac{DR}{RA}\frac{AR}{RB}=1$$
三角形と,その頂点を通らない直線の配置は上図のように $2$ パターンあります.ひとつは,直線が三角形の $2$ 辺と交わる場合で,もうひとつは三角形と交わらない場合です.そのどちらについてもメネラウスの定理は成り立ちます.上の証明はどちらの図の状況に対しても成り立つことを確認してみてください.
メネラウスの定理は逆の主張が成り立ちます.証明にはメネラウスの定理を用います.
メネラウスの定理の逆: $△ABC$ の辺 $BC,CA,AB$ またはそれらの延長上に,それぞれ点 $P,Q,R$ があり,この $3$ 点のうち,$1$ 個または $3$ 個が辺の延長上の点であるとする.このとき, $$\frac{BP}{PC}\frac{CQ}{QA}\frac{AR}{RB}=1$$ が成り立つならば,$3$ 点 $P,Q,R$ は一直線上にある.
証明: 直線 $QR$ と辺 $BC$ の延長との交点を $P’$ とすると,メネラウスの定理より, $$\frac{BP’}{P’C}\frac{CQ}{QA}\frac{AR}{RB}=1$$ 仮定より, $$\frac{BP}{PC}\frac{CQ}{QA}\frac{AR}{RB}=1$$ よって,$$\frac{BP}{PC}=\frac{BP’}{P’C}$$ $P,P’$ はともに辺 $BC$ の延長上の点なので,$P’$ は $P$ に一致する. よって,$3$ 点 $P,Q,R$ は一直線上にある.
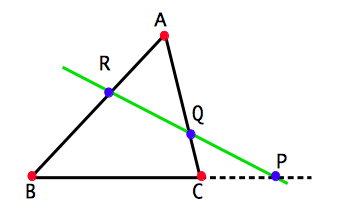
メネラウスの定理は一見複雑なように見えますが,あるコツさえ知っていればいつでも迷うことなく立式できます.まず,メネラウスの基本は三角形と一つの直線です.ここで,直線と三角形の辺 (またはその延長) の交点を分点と呼ぶことにします.つまり,点 $P,Q,R$ が分点です.図では,わかりやすいように頂点は赤色,分点は青色で書いています.そこで,メネラウスの定理の左辺の式は,ある頂点から出発して,分点と頂点を交互にたどっていくことで,簡単に立てることができます.
たとえば,下図において,メネラウスの式は, $$\frac{BP}{PC}\frac{CQ}{QA}\frac{AR}{RB}=1$$ ですが,これは,$\color{red}{B}→\color{blue}{P}→\color{red}{C}→\color{blue}{Q}→\color{red}{A}→\color{blue}{R}$ とたどっていきながら分母と分子を書いていけば間違えずに立式できます.やり方は人それぞれなので,自分の好みに合ったやり方をマスターするのがよいでしょう.

メネラウスの定理は忘れたころに必要となってくるイメージがあります.