複素数の世界の美しい等式ド・モアブルの定理の意味を解説します.
ド・モアブルの定理とは,複素数の世界で成り立つ以下の等式のことです.$i$ は当然,虚数単位です.
ド・モアブルの定理: $n$ を整数とする.次の等式が成り立つ. $$(\cos \theta+i \sin \theta)^n=\cos n\theta +i \sin n\theta$$
左辺は絶対値が $1$ の複素数の整数乗です.$n$ は整数であれば,正でも $0$ でも,負でも成り立ちます.この定理を用いれば,複素数の整数乗を簡単に求めることができます.
たとえば, $$\left(\frac{\sqrt{3}+i}{2}\right)^4$$ を計算するとき,単純に掛け算をしようとすると,$4$ 乗の計算が面倒です.ところが,ド・モアブルの定理を用いると, $$\left(\frac{\sqrt{3}+i}{2}\right)^4=\left(\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}\right)^4$$ $$=\cos \frac{2\pi}{3}+i\sin \frac{2\pi}{3}=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$$ というように,$4$ 乗の計算を回避して,簡単に求めることができます.このように,ド・モアブルの定理によって,面倒な積の計算を回避できるのです.
証明は数学的帰納法を用いるのが一般的です.途中で,三角関数の加法定理を用いています.以下の証明では,まず,$n$ が負でない整数の場合を示し,その後,$n$ が負の整数の場合を示しています.$n$ が負の整数の場合を示すときに,$n$ が負でない整数のときの結果を利用しています.
証明: まず,$n$ が負でない整数のときについて,数学的帰納法で示す. $n=0$ のとき,(左辺)=(右辺)=$1$ となるので,等式は成立する. $n=k$ のとき,$(\cos \theta+i \sin \theta)^k=\cos k\theta +i \sin k\theta$ が成り立つと仮定する.
このとき, $$(\cos \theta+i \sin \theta)^{k+1}=(\cos \theta+i \sin \theta)^k(\cos \theta+i \sin \theta)$$ 帰納法の仮定より, $$=(\cos k\theta +i \sin k\theta)(\cos \theta+i \sin \theta)=(\cos k\theta \cos \theta-\sin k\theta\sin \theta)+$$ $$i(\cos k\theta \sin \theta+\sin k\theta \cos \theta)$$ 加法定理より, $$=\cos (k+1)\theta+i\sin (k+1)\theta$$ よって, $$(\cos \theta+i \sin \theta)^{k+1}=\cos (k+1)\theta +i \sin (k+1)\theta$$ が成り立つので,帰納法からすべての負でない整数 $n$ について, $$(\cos \theta+i \sin \theta)^n=\cos n\theta +i \sin n\theta$$ が成り立つ.
次に,$n$ が負の整数のときについて,等式が成り立つことを示す.$n < 0$ より,$n=-m$ とおくと,$m > 0$ であり, $$(\cos \theta+i \sin \theta)^n=(\cos \theta+i \sin \theta)^{-m}=\{(\cos \theta+i \sin \theta)^m \}^{-1}$$ $$=(\cos m\theta +i \sin m\theta)^{-1}=\frac{1}{\cos m\theta +i \sin m\theta}$$ $$=\cos m\theta -i \sin m\theta=\cos (-n)\theta -i \sin (-n)\theta=\cos n\theta+i \sin n\theta$$ となる.したがって,$n$ が負の整数のときも等式が成り立つ.
以上より,すべての整数 $n$ について, $$(\cos \theta+i \sin \theta)^n=\cos n\theta +i \sin n\theta$$ が成り立つことが示せた.
複素数平面を考えれば,ド・モアブルの定理に幾何学的な解釈を与えることができます.
まず,複素数 $z=\cos \theta+i\sin \theta$ というのは,複素数平面上で,単位円上にある点です.この複素数 $z$ を整数乗した $z^n$ というのは,複素数平面上でどのような位置に存在するのでしょうか.ド・モアブルの定理はこの問に明確な答えを与えてくれます. $$(\cos \theta+i \sin \theta)^n=\cos n\theta +i \sin n\theta$$ なので,$z^n=\cos n\theta +i \sin n\theta$ です.この右辺は,単位円上にあり偏角が $n\theta$ である複素数を表しています.したがって,$z^n$ は次の図のような位置にあるのです.
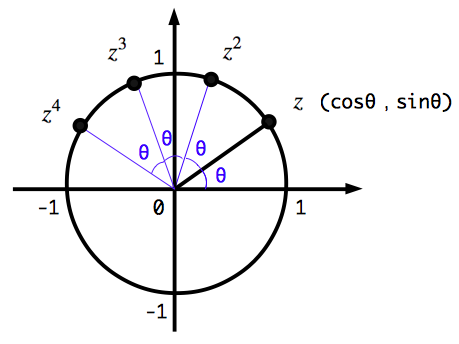
つまり,単位円上にある複素数を整数乗するということは,反時計回りに偏角分回転させていくということなのです.
