座標平面上で,円の方程式はどのようにして表せるでしょうか. まず,原点から距離 $r (r>0)$ の位置にある点 $P(x,y)$ を考えます.
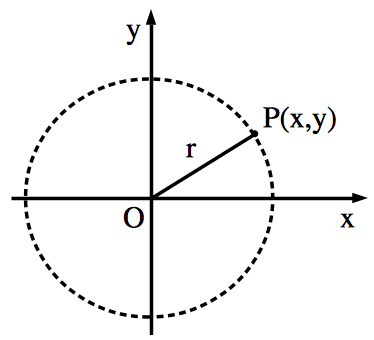
このような点 $P$ の全体 (つまり,原点から距離 $r$ の位置にある点を無数に集めたもの) は原点を中心とする半径 $r$ の円になります.ここで,三平方の定理より,点 $P(x,y)$ について, $$x^2+y^2=r^2$$ が成り立ちます.逆に,座標平面上の点 $P'(x’,y’)$ が $x’^2+y’^2=r^2$ を満たすならば,原点から距離 $r$ の位置にあります.以上より,次が成り立ちます.
原点を中心とする半径 $r$ の円の方程式は次の式で表される. $$x^2+y^2=r^2$$
同様に,点 $(a,b)$ から距離 $r$ の位置にある点 $P(x,y)$ について,三平方の定理より, $$(x-a)^2+(y-b)^2=r^2$$ が成り立ちます.逆も同様に成り立つので,次のことが言えます.
点 $(a,b)$ を中心とする半径 $r$ の円の方程式は次の式で表される. $$(x-a)^2+(y-b)^2=r^2$$
さて,中心の座標と半径が与えられたとき,その円の方程式を表すことができました.ところで,たとえば, $$x^2+y^2+2x+2y+1=0$$ のような方程式が与えられたとき,これが円の方程式かどうか確かめるためにはどうすればよいでしょうか.
左辺を平方完成してみると, $$(x+1)^2+(y+1)^2-1=0$$ となるので, $$(x+1)^2+(y+1)^2=1$$ です.これは,中心 $(-1,-1)$,半径 $1$ の円の方程式を表しています.一方,次の方程式はどうでしょうか. $$x^2+y^2+2x+2y+2=0$$ 左辺を平方完成すると, $$(x+1)^2+(y+1)^2=0$$ となって,これを満たすのは $(x,y)=(-1,-1)$ のみなので,これは $1$ 点 $(-1,-1)$ を表しています.一般に,次のことが成り立ちます.
方程式 $x^2+y^2+lx+my+n=0$ は, $$(x-a)^2+(y-b)^2=r^2$$ の形に変形できるとき,円を表す.
つまり,方程式 $x^2+y^2+lx+my+n=0$ を $x,y$ のそれぞれで平方完成して,$(x-a)^2+(y-b)^2=r^2$ の形にできれば,元の方程式は円を表すということです.実際に,$x^2+y^2+lx+my+n=0$ を平方完成してみると, $$\left(x+\frac{l}{2}\right)^2+\left(y+\frac{m}{2}\right)^2=\frac{l^2+m^2-4n}{4}$$ となります.この右辺が正となれば,方程式は円を表すので,次のことが言えます.
方程式 $x^2+y^2+lx+my+n=0$ が円の方程式であるための必要十分条件は, $$l^2+m^2 > 4n$$ となることである.
与えられた方程式が円を表すかどうか,例題を通して考えてみましょう.
問 次の方程式は円を表すか.
($1$) $x^2+y^2=4$ ($2$) $x^2+y^2=0$ ($3$) $x^2+y^2=-3$
($1$)は円を表す.($2$)は原点を表す.($3$)が表す図形は存在しない.
問 次の方程式は円を表すか.
($1$) $2x^2+y^2=4$ ($2$) $2x^2-2y^2=4$ ($3$) $-3x^2-3y^2=-9$
問 次の方程式は円を表すか.
($1$) $2x^2+3y^2+x=4$ ($2$) $2x^2+2y^2+x+2y=0$ ($3$) $x^2+y^2+2x+y-3=0$