ホッケースティック恒等式 (hockey-stick identity) とは,二項係数に関する等式のひとつです.二項係数に関する等式は数多くありますが,その中でも代表的なもので,非常によく用いられます.この等式を用いると,多くの場面で,数え上げの計算が楽になります.
ホッケースティック恒等式: $n,r$ を $n\ge r$ を満たす自然数とするとき,次の等式が成り立つ. $$\large \sum_{i=r}^n {} _i \mathrm{C} _r ={} _{n+1} \mathrm{C} _{r+1}$$
等式の左辺は,${} _r \mathrm{C} _r$ から ${} _n \mathrm{C} _r$ までの和です.この値が,実は ${} _{n+1} \mathrm{C} _{r+1}$ と等しいことを主張しています.
具体例
・$r=0,n=3$ のとき $$\text{(左辺)}={} _{0} \mathrm{C} _{0}+{} _{1} \mathrm{C} _{1}+{} _{2} \mathrm{C} _{0}+{} _{3} \mathrm{C} _{0}=1+1+1+1=4$$ $$\text{(右辺)}={} _{4} \mathrm{C} _{1}=4$$ となり,確かに等式は成立しています. ・$r=2,n=6$ のとき $$\text{(左辺)}={} _{2} \mathrm{C} _{2}+{} _{3} \mathrm{C} _{2}+{} _{4} \mathrm{C} _{2}+{} _{5} \mathrm{C} _{2}+{} _{6} \mathrm{C} _{2}=1+3+6+10+15=35$$ $$\text{(右辺)}={} _{7} \mathrm{C} _{3}=35$$ となり,確かに等式は成立しています.
二項係数に関する等式証明は,数学的帰納法がうまくいくことが多いです.ホッケースティック恒等式も数学的帰納法で証明できます.ポイントは以下の二項係数に関する公式です.
二項係数に関する公式: $${}_{n} \mathrm{C} _{k} ={}_{n-1} \mathrm{C} _{k-1} +{}_{n-1} \mathrm{C} _{k}$$
この公式の証明は,別記事 →二項係数のいろいろな公式 で紹介しているのでそちらを参考にしてください.上の公式を用いて,ホッケースティック恒等式を証明します.
数学的帰納法による証明: $n$ に関する数学的帰納法で示す. (i) $n=r$ のとき. (左辺)= ${} _r \mathrm{C} _r=1$,(右辺)=${} _{r+1} \mathrm{C} _{r+1}=1$ となり,等式は成立する. (ii) $$\sum_{i=r}^n {} _i \mathrm{C} _r ={} _{n+1} \mathrm{C} _{r+1}$$ が成り立つと仮定する.このとき, $$\sum_{i=r}^{n+1} {} _i \mathrm{C} _r =\sum_{i=r}^n {} _i \mathrm{C} _r +{} _{n+1} \mathrm{C} _{r}$$ $$={} _{n+1} \mathrm{C} _{r+1} +{} _{n+1} \mathrm{C} _{r}\ \ (\because \text{帰納法の仮定})$$ $$={} _{n+2} \mathrm{C} _{r+1}\ \ (\because \text{二項係数に関する公式})$$ したがって,$n+1$ のときも等式は成立する.
以上,(i),(ii) より,等式は示された.
二項係数は,もともと組合せ的な意味をもつ数であることから想像できるように,ホッケースティック恒等式にも,組合せ的な解釈を与えることができます.
場合の数による証明: $n+1$ の人 $A_1,A_2,…,A_{n+1}$ から $r+1$ 人を選ぶ場合の数を $2$ 通りの方法で考える. (i) $n+1$ 人から $r+1$ 人を選ぶ場合の数は ${} _{n+1} \mathrm{C} _{r+1}$ 通りである. (ii) ある $j$ について,$A_j$ を選んで,$A_1,…,A_{j-1}$ を選ばないという状況で場合分けして考える..このような選び方が起こりうる $j$ の範囲は $$1\le j \le n-r+1$$ である.さらに,$n+1$ 人から $r+1$ 人を選ぶとき,『$A_j$ を選んでいて,$A_1,…,A_{j-1}$ を選んでいない』という状況は,必ずただひとつの $j$ に対して起こる. ある $j\ (1\le j \le n-r+1)$ に対して,『$A_j$ を選んで,$A_1,…,A_{j-1}$ を選ばない』場合の数は,$A_{j+1},…,A_{n+1}$ から $r$ 人を選ぶ場合の数に等しいので, $${} _{n+1-j} \mathrm{C} _{r}$$ 通りである. したがって,求める場合の数は, $$\sum_{j=1}^{n-r+1} {} _{n+1-j} \mathrm{C} _{r}$$ 通り. ここで,$i=n+1-j$ と変数変換して,和の取り方を逆順にすると, $$\sum_{j=1}^{n-r+1} {} _{n+1-j} \mathrm{C} _{r}=\sum_{i=r}^n {} _i \mathrm{C} _r$$ を得る.
以上,(i),(ii) より,等式は示された.
ホッケースティック恒等式をパスカルの三角形を通して眺めてみましょう.
パスカルの三角形については,→パスカルの三角形と最短経路で詳しく紹介していますのでそちらを参考にしてください.
下図は,パスカルの三角形を $9$ 段目まで書いたものです.

さて,パスカルの三角形の $n$ 段目 ($n\ge 0$) には, $${} _{n} \mathrm{C} _{0},{} _{n} \mathrm{C} _{1},…,{} _{n} \mathrm{C} _{n}$$ という数が並んでいます.そして,ホッケースティック恒等式の左辺は, $$\sum_{i=r}^n {} _i \mathrm{C} _r$$ という形をしていました.したがって,この式をパスカルの三角形上で考えると,($r$ 段目の左から $r$ 項目)$+$($r+1$ 段目の左から $r$ 項目)$+\cdots +$($n$ 段目の左から $r$ 項目)を表していることになります.
一方,ホッケースティック恒等式の右辺は, $${} _{n+1} \mathrm{C} _{r+1}$$ なので,$n+1$ 段目の左から $r+1$ 項目を表しています. 以上より,ホッケースティック恒等式をパスカルの三角形上で眺めると下図のようになります.
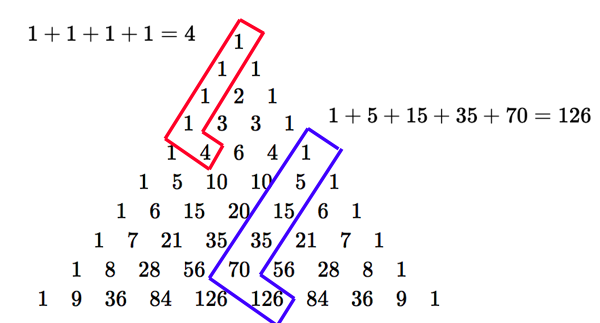
つまり,パスカルの三角形を,右側の辺から左下に向かって斜めに足し合わせた値が,右下に折れ曲がったところの値と一致しているということを言っているのです.
このL字のような形がホッケーのスティックに似ていることが名前の由来です.
問 $5$ 桁の自然数であって,万の位の数が,他の位の数の和であるようなものはいくつあるか.
万の位の数を $k$ とすると,$k$ のとりうる範囲は $1\le k \le 9$ である.各 $k$ に対して,条件をみたすような整数の個数は,$k$ 個の○と $3$ 個の | を一列に並べる場合の数と等しい.(→重複組合せの考え方,) (たとえば,$\circ | \circ | \circ\circ|$ → $41120$ ,$\circ||\circ |\circ$ → $31011$ など) したがって,その場合の数は ${} _{k+3} \mathrm{C} _{3}$ 通り.
よって,求める場合の数は, $$\sum_{k=1}^9 {} _{k+3} \mathrm{C} _{3} = \left(\sum_{k=0}^9 {} _{k+3} \mathrm{C} _{3} \right) -1={} _{13} \mathrm{C} _{4}-1=714$$ $714$ 個.
問 多項式 $1+(1-x)+(1-x)^2+\cdots +(1-x)^{15}$ を実数 $a_0,…,a_{15}$ を用いて $$a_0+a_1x+a_2x^2+\cdots +a_{15}x^{15}$$ と表すとき,$a_2$ の値を求めよ.
各 $k\ (2\le k \le 15)$ に対して,$(1-x)^{k}$ の $x^2$ の係数は,二項定理より, $${} _{k} \mathrm{C} _{2}$$ である.したがって, $$a_2=\sum_{k=2}^{15} {} _{k} \mathrm{C} _2={} _{16} \mathrm{C} _3=560$$
問 集合 $\{1,2,…,2020\}$ の要素数 $1000$ の部分集合全体を考える.各部分集合における最小の要素の相加平均 $M$ を求めよ.
集合 $\{1,2,…,2020\}$ の要素数 $1000$ の部分集合はぜんぶで ${} _{2020} \mathrm{C} _{1000}$ 個ある.
$\{1,2,…,2020\}$ から要素数 $1000$ の部分集合をとりだしたとき,その部分集合の最小の要素を $k$ とする.$k$ としてとりうる範囲は $1\le k \le 1021$ である.各 $k$ に対して,最小の要素が $k$ であるような要素数 $1000$ の部分集合の個数は,$k+1\sim2020$ から $999$ 個選ぶ場合の数に等しいので, $${} _{2020-k} \mathrm{C} _{999}$$ 個である.よって, $${} _{2020} \mathrm{C} _{1000} M=\sum_{k=1}^{1021} {} _{2020-k} \mathrm{C} _{999}\cdot k$$ が成り立つ.ここで,右辺は, $$\sum_{k=1}^{1021} {} _{2020-k} \mathrm{C} _{999}\cdot k$$ $$={} _{2020-1} \mathrm{C} _{999}$$ $$+{} _{2020-2} \mathrm{C} _{999}+{} _{2020-2} \mathrm{C} _{999}$$ $$+{} _{2020-3} \mathrm{C} _{999}+{} _{2020-3} \mathrm{C} _{999}+{} _{2020-3} \mathrm{C} _{999}$$ $$+\ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ +\ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ +\ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ $$ $$+{} _{2020-1021} \mathrm{C} _{999}+{} _{2020-1021} \mathrm{C} _{999}+\cdots +{} _{2020-1021} \mathrm{C} _{999}$$ であるが,これらの和を縦向きに足して,ホッケースティック恒等式を用いると, $$={} _{2020} \mathrm{C} _{1000}+{} _{2019} \mathrm{C} _{1000}+\cdots +{} _{1000} \mathrm{C} _{1000}$$ 再び,ホッケースティック恒等式を用いると, $$={} _{2021} \mathrm{C} _{1001}$$ 以上より, $$M=\frac{{} _{2021} \mathrm{C} _{1001}}{{} _{2020} \mathrm{C} _{1000}}=\frac{1000!1020!}{2020!}\cdot \frac{2021!}{1001!1020!}=\frac{2021}{1001}$$ よって,$M=\frac{2021}{1001}$.

