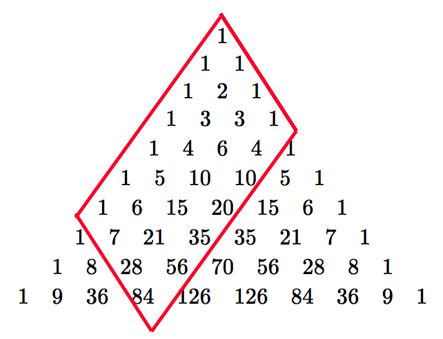
二項係数の値の視覚化である，パスカルの三角形を紹介します．
唐突ですが，下図をご覧ください．
$0$ 段目に $1$ という数が書かれており，$1$ 段目に $1\ 1$，$2$ 段目に $1\ 2\ 1$ ，$3$ 段目に $1\ 3\ 3\ 1$，という風に $n$ 段目に $n+1$ 個の数が書かれています．$n$ 段目の $n+1$ 個の数をここでは，左から第 $0$ 項，第 $1$ 項，．．．，第 $n$ 項と呼ぶことにします．(図では $9$ 段目までしか書かれていませんが，本当はずっと続きます) これはつぎのようにしてつくることができます． $Step\ 0:$ $0$ 段目に $1$ を書く． $Step\ 1:$ $n$ 段目 ($n \ge 1$)の左端と右端には $1$ を書く． $Step\ 2:$ $n+1$ 段目 ($n \ge 1$) の左から $k$ 項目 ($1\le k \le n$) に，$n$ 段目の左から $k-1$ 項目と $k$ 項目の和を書く．
このような手続きでつくられる図形をパスカルの三角形と呼びます．(つまり，上図はパスカルの三角形の $9$ 段目までを描いたものです)
つくりかたの $Step\ 2$ より，隣合う $2$ つの数の和がそのすぐ下の数になります．
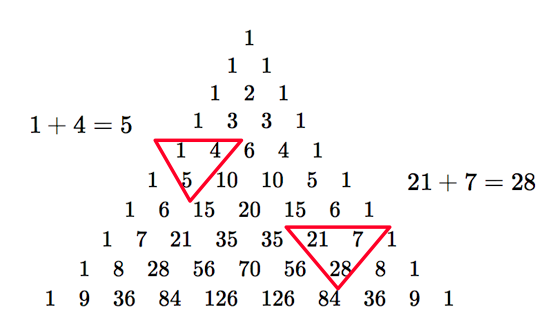
実は，パスカルの三角形の $n$ 段目の左から $k$ 項目の数は，二項係数 ${}_n \mathrm{C} _k$ に一致します． このことは，二項係数のつぎの性質からわかります．(この公式については →二項係数のいろいろな公式を参照してください)
二項係数の性質： $$\large {}_{n+1} \mathrm{C} _{k} ={}_{n} \mathrm{C} _{k-1} +{}_{n} \mathrm{C} _{k}$$
なぜなら，まず，二項係数の定義から ${}_0 \mathrm{C} _0=1，{}_n \mathrm{C} _0={}_n \mathrm{C} _n=1$ などが成り立ちます．これはパスカルの三角形の作り方における，$Step\ 1$ と $Step\ 2$ に対応します．そして，${}_{n+1} \mathrm{C} _{k} ={}_{n} \mathrm{C} _{k-1} +{}_{n} \mathrm{C} _{k}$ が $Step\ 3$ に対応します．つまり，パスカルの三角形は実は二項係数の値の表だったのです！
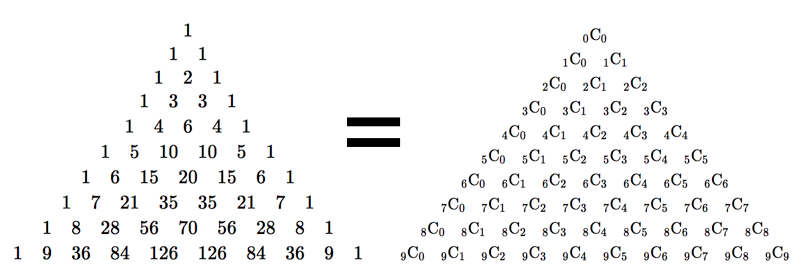パスカルの三角形が二項係数の表であり，二項係数は ${}_n \mathrm{C} _k=\frac{n!}{k!(n-k)!}$ と計算できるのに，なぜこのようなものを考える必要があるのでしょうか．なにがうれしいのでしょうか．
この問いの解答はいくつか考えられます．ひとつは，複数の二項係数の値を一気に得られることでしょう．確かに，個々の二項係数の値は公式 ${}_n \mathrm{C} _k=\frac{n!}{k!(n-k)!}$ で計算できます．しかし，比較的小さな $n$ に対して，${}_n \mathrm{C} _0,{}_n \mathrm{C} _1,{}_n \mathrm{C} _2,{}_n \mathrm{C} _3,\cdots,{}_n \mathrm{C} _n$ をすべて知りたいときなどはパスカルの三角形を用いたほうが早いです．パスカルの三角形は手を動かしてつくりやすいのです．(ぜひ実際にやってみてください．$10$ 段目ぐらいまでなら $1$ 分もかからずにつくれるでしょう)
他にもここでは紹介しませんが，偶奇だけに着目するとフラクタル構造が現れるなど，パスカルの三角形を考えることによって新たに理解できることは多くあります．大切なことは，パスカルの三角形によって，個々の二項係数たちを構造的に，組織的に眺めることができるということです．そのような新しい視点を与えてくれるのです．
パスカルの三角形のもっとも簡単な応用は二項展開です．これはつぎの二項定理に基づいています．
二項定理： $$\large (x+y)^n=\sum_{k=0}^n {}_n \mathrm{C} _k x^ky^{n-k}$$
これより，$(x+y)^n$ を展開したときの各項の係数は，二項係数になります．特に，展開の結果を知るには，${}_n \mathrm{C} _0,\cdots ,{}_n \mathrm{C} _n$ の値をすべて知れば十分です．
たとえば，$(x+y)^6$ の展開は，パスカルの三角形を $6$ 段目までつくることにより， $$(x+y)^6=x^6 + 6 x^5 y + 15 x^4 y^2 + 20 x^3 y^3 + 15 x^2 y^4 + 6 x y^5 + y^6$$ と導けます．$(x+y)^{10}$ は $10$ 段目を見れば， $$(x+y)^{10}=x^{10} + 10 x^9 y + 45 x^8 y^2 + 120 x^7 y^3 + 210 x^6 y^4 $$ $$+ 252 x^5 y^5 + 210 x^4 y^6 + 120 x^3 y^7 + 45 x^2 y^8 + 10 x y^9 + y^{10}$$ と導けます．
先にみた二項係数の性質 ${}_{n+1} \mathrm{C} _{k} ={}_{n} \mathrm{C} _{k-1} +{}_{n} \mathrm{C} _{k}$ はよくある最短経路問題に応用できます．中学受験を経験した方はなんとなく知っている話かと思います．つぎの問題を考えてみましょう．
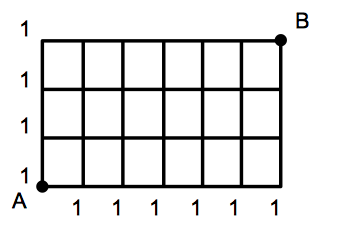
例題 下図のような格子状の街路がある．地点 $A$ から地点 $B$ まで最短の経路で行く方法は何通りあるか．
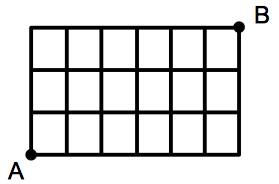
組合せの知識を知っていれば，${}_9 \mathrm{C} _3=84$ で $84$ 通りとすぐに求められるのですが，ここではあえて別の方法で解きます． まず，下図のように，$A$ からまっすぐ上にいってたどりつける地点と，まっすぐ右にいってたどりつける地点すべてに $1$ という数を割り振ります．
つぎに，まだ数が割り振られていない地点には，そのすぐ左の地点とすぐ下の地点に割り振られた数の和を割り振ります．このようにして，すべての地点に数を割り振ります．すると，地点 $B$ に割り振られた数が，$A$ から $B$ までの最短で行く方法の総数になるのです．
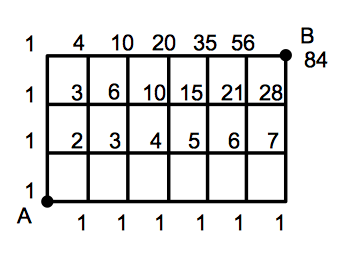実は，どの地点についても，そこに割り振られた数は，$A$ からその地点へ最短で行く方法の総数になっています．これは次のように考えれば理解できます． まず，$A$ から，はじめに $1$ と割り振った地点へ行く方法が $1$ 通りであることは明らかです．(最短で行く方法を聞いているので，遠回りできないことに注意してください) さて，つぎにその他の地点の割り振り方です．どの地点についても，そこへ最短で行くには，左からくるか，下からくるかの $2$ 通りしかありえません．そしてそれらは同時には起こりえません．したがって，和の法則により， $$\text{(ある地点} P \text{へ最短で行く方法の総数)}=\text{(左から} P \text{へ最短で行く方法の総数)}+\text{(下から} P \text{へ最短で行く方法の総数)}$$ が成り立ちます．これが，上の方法の原理になっています．そしてこの方法は，パスカルの三角形のつくりかたと全く同じです．したがって，この割り振られた数たちはパスカルの三角形に部分的な構造と一致しているのです．
