三角関数の積和・和積公式とその導出を紹介し,最後に積和公式の図形的な説明の一例を解説します.
三角関数の積和・和積公式は,三角関数の積を和に,和を積に変換する公式です.これらの公式は三角関数の加法定理から導かれます. 加法定理や,倍角,半角の公式に比べて使用頻度は多くありませんが,教科書に載っている公式なので,覚えておくべきです.ただし,たとえこの公式を忘れたとしても,加法定理からすぐに導けます.
積和公式とは,三角関数の積を和に変換するつぎの公式のことです.
積和公式: $$\large \sin\alpha \cos\beta=\frac{1}{2}\left(\sin(\alpha+\beta)+\sin(\alpha-\beta)\right)$$ $$\large \cos\alpha \sin\beta=\frac{1}{2}\left(\sin(\alpha+\beta)-\sin(\alpha-\beta)\right)$$ $$\large \cos\alpha \cos\beta=\frac{1}{2}\left(\cos(\alpha+\beta)+\cos(\alpha-\beta)\right)$$ $$\large \sin\alpha \sin\beta=-\frac{1}{2}\left(\cos(\alpha+\beta)-\cos(\alpha-\beta)\right)$$
例
・積和公式を用いて,$\sin 45°\cos 15°$ の値を求めます. $$\sin 45°\cos 15°=\frac{1}{2}(\sin (45°+15°)+\sin (45°-15°))=\frac{1}{2}(\sin 60°+\sin 30°)=\frac{1}{2}(\frac{\sqrt{3}}{2}+\frac{1}{2})=\frac{\sqrt{3}+1}{4}$$
逆に,和積公式とは,三角関数の和を積に変換する公式のことです.
和積公式: $$\large \sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$$ $$\large \sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2}$$ $$\large \cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$$ $$\large \cos A-\cos B=2\sin\frac{A+B}{2}\sin\frac{A-B}{2}$$
例
・和積公式を用いて,$\sin 75°+\sin 15°$ の値を求めます. $$\sin 75°+\sin 15°=2\sin \frac{75°+15°}{2}\cos \frac{75°-15°}{2}=2\sin 45°\cos 30°=\frac{\sqrt{6}}{2}$$
注意
積和公式,和積公式という $2$ つの公式があるように書いていますが,実はこれら $2$ つの公式は同じものです.つまり,一方を変数変換することで他方が導かれます.実際,積和公式において,$A=\alpha+\beta,B=\alpha-\beta$ とおくと,$\alpha=\frac{A+B}{2},\beta=\frac{A-B}{2}$ なので,積和公式のそれぞれの式が和積公式のそれぞれの式に対応します.
全く同じ公式をわざわざ$2$ つの公式に分けているのは,主語を明確に区別するためだと思われます.数学では一般に,等式の左辺を主語だと思う慣習があります.つまりここでは,積和公式は三角関数の積が主語だと思っており (積は和に変換できる),和積公式では三角関数の和が主語だと思っている (和は積に変換できる) という違いにすぎません.
積和・和積公式はすべて,三角関数の加法定理から導かれます.前節の注意で述べたように,和積公式は積和公式を変数変換しただけなので,ここでは,積和公式の導出のみ行います.
公式の導出: $\sin$ の加法定理より, $$\sin(\alpha+\beta)=\sin \alpha \cos \beta +\cos \alpha\sin \beta \cdots (1)$$ $$\sin(\alpha-\beta)=\sin \alpha \cos \beta -\cos \alpha\sin \beta \cdots (2)$$ が成り立つ.($1$)+($2$) より, $$\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin \alpha\cos \beta$$ したがって, $$\boxed{\sin\alpha \cos\beta=\frac{1}{2}\left(\sin(\alpha+\beta)+\sin(\alpha-\beta)\right)}$$ を得る. また,($1$)-($2$) より, $$\sin(\alpha+\beta)-\sin(\alpha-\beta)=2\cos \alpha\sin \beta$$ したがって, $$\boxed{\cos\alpha \sin\beta=\frac{1}{2}\left(\sin(\alpha+\beta)-\sin(\alpha-\beta)\right)}$$ を得る.
$\cos$ の加法定理より, $$\cos(\alpha+\beta)=\cos \alpha\cos \beta-\sin \alpha\sin \beta \cdots (3)$$ $$\cos(\alpha-\beta)=\cos \alpha\cos \beta+\sin \alpha\sin \beta \cdots (4)$$ が成り立つ.($3$)+($4$) より, $$\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos \alpha\cos \beta$$ したがって, $$\boxed{\cos\alpha \cos\beta=\frac{1}{2}\left(\cos(\alpha+\beta)+\cos(\alpha-\beta)\right)}$$ を得る.また,($3$)-($4$) より, $$\cos(\alpha+\beta)-\cos(\alpha-\beta)=-2\sin \alpha\sin \beta$$ したがって, $$\boxed{\sin\alpha \sin\beta=-\frac{1}{2}\left(\cos(\alpha+\beta)-\cos(\alpha-\beta)\right)}$$ を得る.
最後におまけとして,和積公式 $$\large \sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$$ $$\large \cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$$ をベクトルを用いて導出する方法を紹介します. $A=B$ のときは和積公式は明らかに成り立つので,$A\neq B$ と仮定しておきます. まず,下図のような図形を考えます.点 $P,Q$ は $x$ 軸の正の部分を始線として,それぞれ角 $A,B$ をなす直線と単位円との交点です.また,点 $R$ は四角形 $OPRQ$ が平行四辺形となるような点です.
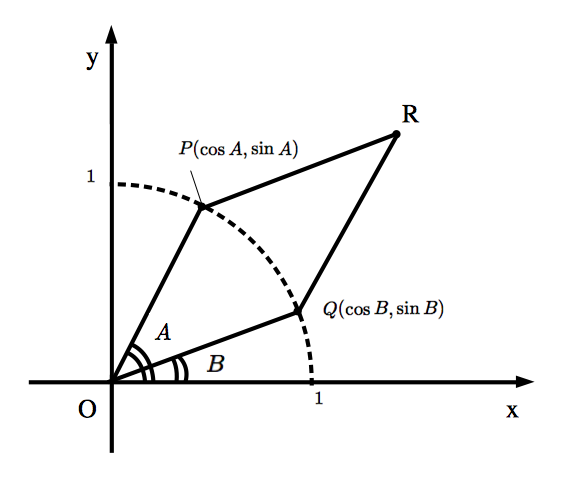
$R$ の座標を $2$ 通りの方法で表すことによって,和積公式を導きます. まず,$P (\cos A,\sin A),Q (\cos B,\sin B)$ なので, $$\overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{OQ}=(\cos A+\cos B,\sin A+\sin B)$$ したがって,$R (\cos A+\cos B,\sin A+\sin B) \cdots (1)$ です. さてつぎに,$OR$ と $PQ$ の交点を $S$,$OR$ と単位円との交点を $T$ とします.
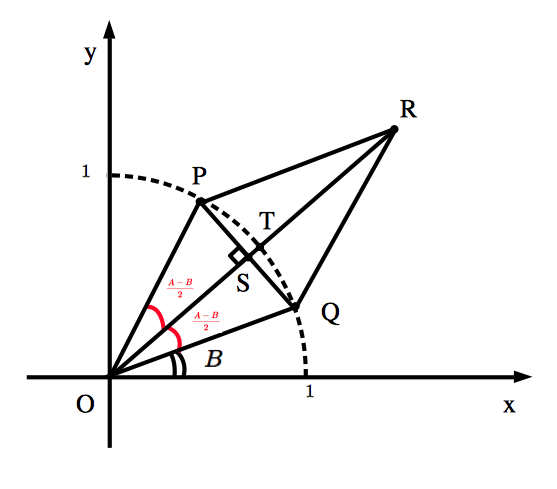
このとき, $$\overrightarrow{OR}=2\times \overrightarrow{OS}=2\times \overrightarrow{OT}\times \frac{|\overrightarrow{OS}|}{|\overrightarrow{OT}|} \cdots (*)$$ が成り立ちます.また, $$\angle POT=\angle QOT=\frac{A-B}{2}$$ であることに注意すると, $$|\overrightarrow{OT}|=1$$ $$|\overrightarrow{OS}|=|\overrightarrow{OP}|\times \cos \angle POS=\cos \frac{A-B}{2}$$ $$\overrightarrow{OT}=(\cos \frac{A+B}{2},\sin \frac{A+B}{2})$$ などがわかります.これらを ($*$) へ代入すると, $$\overrightarrow{OR}=(2\cos\frac{A+B}{2}\cos\frac{A-B}{2},2\sin\frac{A+B}{2}\cos\frac{A-B}{2})$$ が成り立ちます.したがって, $$R(2\cos\frac{A+B}{2}\cos\frac{A-B}{2},2\sin\frac{A+B}{2}\cos\frac{A-B}{2}) \cdots (2)$$ $(1)$ と $(2)$ の $x$ 座標と $y$ 座標を比べると, $$\large \sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$$ $$\large \cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$$ が導かれます.

