高校数学ではあまり話題になることが少ない三角不等式について，一歩踏み込んでみましょう．ここでいう三角不等式とは，三角比を含む不等式のことではありません．
三角不等式とは，実数，複素数，ベクトルなどにおける絶対値に関する不等式のことです．大学数学などでは頻繁に用いられる基本的な不等式です．まれに，大学入試の問題でも三角不等式を背景にもつ問題が見られます．
三角不等式: $x,y$ を実数とする．次の不等式が成り立つ． $$||x|-|y|| \le |x+y| \le |x|+|y|$$
証明: $$(|x|+|y|)^2-(|x+y|)^2=(x^2+2|x||y|+y^2)-(x+y)^2$$ $$=2(|x||y|-xy) \ge 0$$ であり，$|x|+|y|,|x+y|$ はともに $0$ 以上であるから， $$|x+y| \le |x|+|y| \cdots(1)$$ が成り立つ．また，($1$) 式の $x$ に $x+y$ を，$y$ に $-y$ を代入すると， $$|x| \le |x+y|+|-y|$$ となる．$|-y|=|y|$ であることに注意すると， $$|x|-|y| \le |x+y| \cdots(2)$$ 同様にして ($1$) 式に，$x$ に $-x$ を，$y$ に $x+y$ を代入すると， $$|y| \le |-x|+|x+y|$$ となるので， $$|y|-|x| \le |x+y| \cdots(3)$$ ($2$),($3$) を合わせると， $$||x|-|y|| \le |x+y|.$$ 以上より， $$||x|-|y|| \le |x+y| \le |x|+|y|$$
右側の不等式 $|x+y| \le |x|+|y|$ が大切で，左側の不等式 $||x|-|y|| \le |x+y|$ はおまけです．
証明ではまず，右側の不等式が成り立つことを示し，そのあとにその不等式を再利用して，左側の不等式を示しました．このようにしなくても左側の不等式が成り立つことは示せますが，ちょっとした省エネになっています．さて，ここでは証明は省略しますが，複素数やベクトルに対しても同様の式が成り立ちます．複素数 $z=x+yi$ ($x,y$ は実数) に対して，$|z|=\sqrt{x^2+y^2}$ です．また，ベクトル $\vec{a}=(a_1,a_2,a_3)$ に対して，$|\vec{a}|=\sqrt{a_1^2+a_2^2+a_3^2}$ です．
三角不等式(複素数版): $z,w$ を複素数とする．次の不等式が成り立つ． $$||z|-|w|| \le |z+w| \le |z|+|w|$$
三角不等式(ベクトル版): ベクトル $\vec{a},\vec{b}$ に対して，次の不等式が成り立つ． $$||\vec{a}|-|\vec{b}|| \le |\vec{a}+\vec{b}| \le |\vec{a}|+|\vec{b}|$$
ちょっとした発展形として，上で示した三角不等式を有限回用いると，帰納的に以下の不等式が導かれます．
三角不等式(拡張版): $n$ 個の複素数 $x_1,…,x_n$ に対して，次の不等式が成り立つ． $$|x_1+x_2+\cdots +x_n| \le |x_1|+|x_2|+\cdots+|x_n|$$
三角不等式から，距離に関する基本的な事実が導かれます．いま，複素数平面上に異なる $3$ 点 $A_1(z_1),A_2(z_2),A_3(z_3)$ があるとします(単に平面でも構いませんが，簡単のため複素数平面を考えます)．当然ですが，
地点 $A_1$ から地点 $A_2$ へ直線で行く距離は，$A_1$ から $A_3$ へ寄り道してから $A_2$ へ行く距離より短いです．
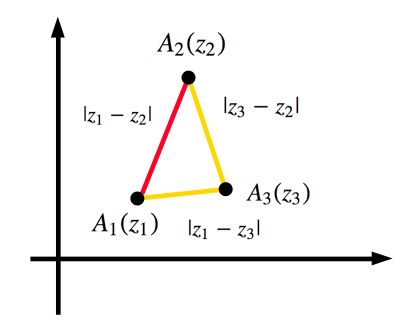この事実は先の複素数版の三角不等式 $|z+w| \le |z|+|w|$ において，$z$ に $z_1-z_3$ を， $w$ に $z_3-z_2$ を代入することで得られる式を考えるとよくわかります．
$3$ つの複素数 $z_1,z_2,z_3$ に対して，次の不等式が成り立つ． $$|z_1-z_2| \le |z_1-z_3|+|z_3-z_2|$$
最後に三角不等式の図形的な意味を見てみましょう．実数よりも，複素数のほうがその意味合いが感覚的にわかりやすいので，複素数版の方で考えます．複素数平面上に $2$ 点 $P(z),Q(w)$ があるとします．
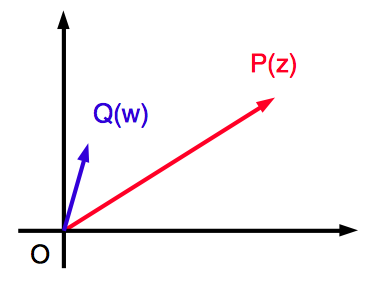$|OP|=|z|,|OQ|=|w|$ です．ここで，$\overrightarrow{OQ}$の始点を点 $P$ にもってきます．さらに $P$ を中心とする半径 $|w|$ の円 $C$ を破線で描くと，下図のようになります．
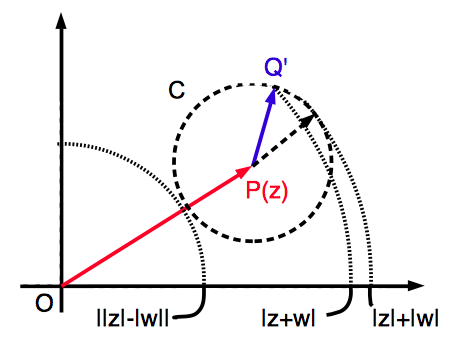
細かい破線で書かれた円弧はすべて原点 $O$ を中心とする円の一部で,一番半径が小さい円弧は円 $C$ に外接するように描かれていて，二番目の円弧は半径が $|\overrightarrow{OQ’}|$ となるように描かれていて，最も半径が大きい円弧は円 $C$ に内接するように描かれています．この図を見れば， $$||z|-|w|| \le |z+w| \le |z|+|w|$$ は一目瞭然です．
以上，三角不等式にまつわる事柄を見てきました．この不等式は大学数学では大活躍するのですが，高校数学ではマイナーなので悲しいです．
