２点を内分する点，外分する点の座標の求め方を解説します．
直線上や，平面上，空間上で相異なる $2$ 点が与えられた時，それらを内分する点や外分する点を考えることができます． たとえば，線分ABを $2:1$ に内分する点とは，線分 $AB$ 上で，$A$ からの距離と $B$ からの距離の比が $2:1$ であるような点のことを指します．
$2$ 点の座標が与えられた時，その $2$ 点を内分する点，外分する点の座標の求め方を考えてみましょう．
まずは，数直線上に相異なる $2$ 点 $A(a),B(b)$ がある場合を考えましょう．この場合，$A,B$ の並び方は下図のように左から $A,B$ と並ぶ場合と，左から $B,A$ と並ぶ場合の $2$ 通りあります．
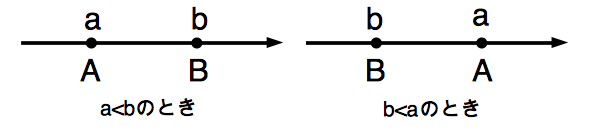
いずれの場合についても次が成り立ちます．
線分の内分点，外分点: 数直線上の $2$ 点 $A(a),B(b)$ について，線分 $AB$ を $m:n$ に内分する点を $P$，$m:n$ に外分する点を $Q$ とすると， $$\large 点Pの座標は \frac{na+mb}{m+n}， 点Qの座標は \frac{-na+mb}{m-n}$$
上の $2$ つの公式が成り立つことをそれぞれ実際に確かめてみましょう．
内分点について
$A,B$ を $m:n$ に内分する点 $P(x)$ の座標を求めましょう．
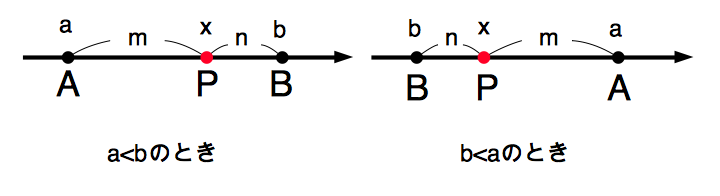$x$ を $a,b,m,n$ を用いて表すのが目標です．線分 $PA$ の長さは $|x-a|$，線分 $PB$ の長さは$|b-x|$ です．$P$ は線分 $AB$ を内分する点なので， $$PA:PB=m:n$$ が成り立ちます．したがって， $$|x-a|:|b-x|=m:n$$ です．これより， $$m|b-x|=n|x-a|$$ となります．ところで，上図の $２$ 通りのどちらの場合についても，$|x-a|$ と $|b-x|$ は同符号です．したがって，上式の絶対値記号をそのまま外すことができて， $$m(b-x)=n(x-a)$$ が成り立ちます．これを整理すると， $$x=\frac{na+mb}{m+n}$$ となって，実際に公式が成り立つのがわかります．
特に，$m=n=1$ の場合は，点 $P$ は線分 $AB$ の中点で，その座標は $\frac{a+b}{2}$ です．
外分点について
まず，$m>n>0$ とします． $A,B$ を $m:n$ に外分する点 $Q(x)$ の座標を求めましょう．
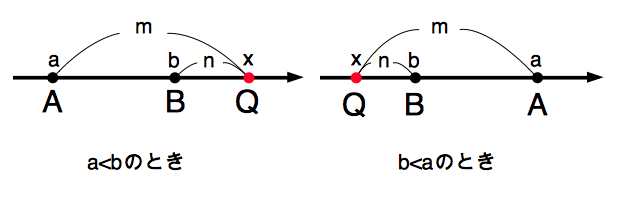
$x$ を $a,b,m,n$ を用いて表すのが目標です．線分 $QA$ の長さは $|x-a|$，線分 $QB$ の長さは$|b-x|$ です．$P$ は線分 $AB$ を外分する点なので， $$QA:QB=m:n$$ が成り立ちます．したがって， $$|x-a|:|b-x|=m:n$$ です．これより， $$m|b-x|=n|x-a|$$ となります．ところで，上図の $２$ 通りのどちらの場合についても，$|x-a|$ と $|b-x|$ は異符号です．したがって，上式の絶対値記号は，一方にマイナス符号をつけて外すことができて， $$m(b-x)=-n(x-a)$$ が成り立ちます．これを整理すると， $$x=\frac{-na+mb}{m-n}$$ となって，実際に公式が成り立つのがわかります．
$0< m< n$ のときも同様にして示すことができます．
座標平面上の相異なる $2$ 点 $A(x_1,y_1),B(x_2,y_2)$ について，次が成り立ちます．
平面上の内分点，外分点の座標: $2$ 点 $A(x_1,y_1)，B(x_2,y_2)$ について，線分 $AB$ を $m:n$ に内分する点を $P$，$m:n$ に外分する点を $Q$ とすると， $$\large 点Pの座標は \left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)$$ $$\large 点Qの座標は \left(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\right)$$
$x$ 座標，$y$ 座標のそれぞれが，数直線上での公式と同じ形になっています．上の公式は次のように確認できます． たとえば内分点については，下図のように，$A,B$ が配置してあるとき，$A,B,P$ から $x$ 軸に垂線 $AA’,BB’,PP’$ をひくと，$P’$ は線分 $A’B’$ を $m:n$ に内分します．
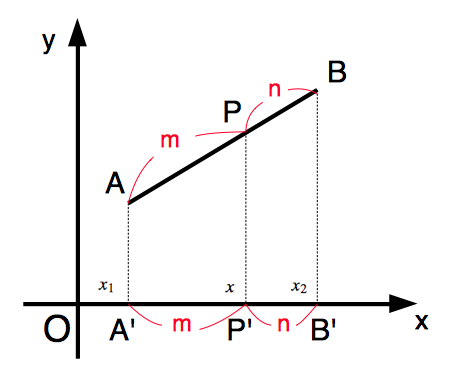
したがって，前節での考察によって， $$x=\frac{nx_1+mx_2}{m+n}$$ が成り立ちます．$y$ 座標についても同様です．$AB$ が $y$ 軸や $x$ 軸に垂直なときも公式が成り立つことは容易に確認できます．
