Spernerの補題とは,ブラウワーの不動点定理の組合せ的なアナロジーとして知られている命題です. 本記事ではブラウワーの不動点定理との関連は解説せずに,Spernerの補題の主張と証明を紹介します.
Spernerの補題はそれ自体面白い命題で,意味と証明を理解するために特別な知識は使いません. より一般化された形でのSpernerの補題も存在しますが,この記事では簡単のために $1$ 次元版と $2$ 次元版に限って紹介します.
はじめに,$1$ 次元版のSpernerの補題を紹介します. 次のような状況を考えてみましょう. 直線上に $2$ 個以上の有限個の点が与えられているとします.
これらすべての点に対して,次のルールを満たすように赤または青の色を割り当てます.
$Rule~1$ : 両端は相異なる色を割り当てる.
$Rule~2$ : 両端以外の点は赤または青を割り当てる.
つまり両端だけ異なる色を割り当て,それ以外の点は好きなように $2$ 色を割り当てます. このとき,異なる色が割り当てられた隣り合う $2$ 点が必ず存在します.これが $1$ 次元版のSpernerの補題の主張です.
まとめると,次のようになります.
Spernerの補題(1次元版):直線上に有限個の点集合 $S$ が与えられる.ただし,$|S|\ge 2$ とする.$S$ の各点に対して,次のルールを満たすような $2$ 色 (赤,青) の色割り当てを考える. $Rule~1$ : 両端は相異なる色を割り当てる.
$Rule~2$ : 両端以外の点は赤または青を割り当てる.
このとき,異なる色が割り当てられた隣り合う $2$ 点が必ず存在する.
いくつかの具体例をみてみると,確かにこの補題の主張が成り立っていることが確認できます.
具体例
証明
さて,この補題はつぎのように簡単に示すことができます.
Spernerの補題(1次元版)の証明: 有限個の頂点を左端から順に $x_1,…,x_n$ とする. 左端から順に点をみていき,はじめて青が割り当ている点を $x_i$ とする.$x_n$ が青色なので,このような点 $x_i$ は必ず存在する.また,$x_1$ は赤色なので,$2\le i \le n$ である.さらに $x_i$ ははじめて青色となる点であるから,$x_{i-1}$ は赤色である.したがって,$2$ 点 $x_{i-1},x_{i}$ は異なる色が割り当てられた隣り合う $2$ 点である.
さらに,このような異なる色が割り当てられた隣り合う $2$ 点のペアは奇数個であることもすぐに示せます.(興味のある人は証明をチャレンジしてみてください!) この事実は $2$ 次元版のSpernerの補題の証明の際に利用します.
つぎに,$2$ 次元版のSpernerの補題を紹介します.ここからが本題です.$2$ 次元版は $1$ 次元版よりも非自明で,より不思議な感じがすると思います. 今度は平面上の三角形 $ABC$ を考えます.この $\triangle ABC$ 上 ($\triangle ABC$ の境界と内部) に $A,B,C$ を含む有限個の点集合 $S$ が与えられます.
下図のように,$S$ によって $\triangle ABC$ は必ず三角形分割することができます.(これがなぜなのかは省略します.)
さてここで,有限個の点集合 $S$ のすべての点に対して,次のルールを満たすように $3$ 色の色 (赤,青,緑) を割り当てます.
$Rule~1$ : 頂点 $A$ は赤,頂点 $B$ は青,頂点 $C$ は緑を割り当てる.
$Rule~2$ : 線分 $AB$ 上の頂点は赤または青,線分 $BC$ 上の頂点は青または緑,線分 $CA$ 上の頂点は緑または赤を割り当てる.
$Rule~3$ : 内部の頂点は赤または青または緑を割り当てる. このとき,$3$ 頂点に割り当てられた色が相異なるような三角形 (小三角形) が必ず存在します.(下図でオレンジ色の三角形) これが $2$ 次元版のSpernerの補題の主張です.
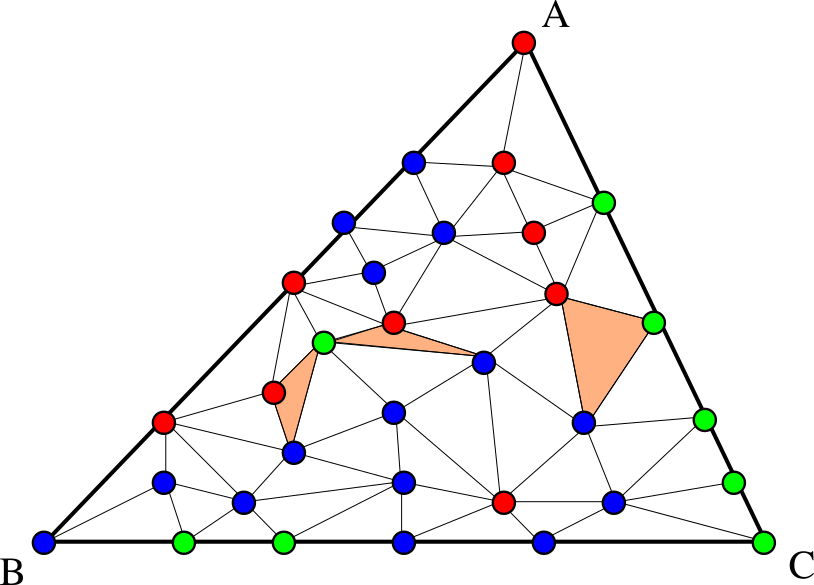
まとめると,つぎのようになります.
Spernerの補題(2次元版): $\triangle ABC$ 上に $A,B,C$ を含む有限個の点集合 $S$ と $S$ による三角形分割が与えられる.$S$ の各点に対して,次のルールを満たすような $3$ 色 (赤,青,緑) の色割り当てを考える.
$Rule~1$ : 頂点 $A$ は赤,頂点 $B$ は青,頂点 $C$ は緑を割り当てる.
$Rule~2$ : 線分 $AB$ 上の頂点は赤または青,線分 $BC$ 上の頂点は青または緑,線分 $CA$ 上の頂点は緑または赤を割り当てる.
$Rule~3$ : 内部の頂点は赤または青または緑を割り当てる.
このとき,$3$ 頂点に割り当てられた色が相異なるような三角形が必ず存在する.
$2$ 次元版のSpernerの補題を証明してみましょう.$1$ 次元版よりもやや議論が必要ですが,特別な知識は用いません.証明のポイントは有限性です.
証明: 端点に赤と青が割り当てられたすべての辺に対し,その辺を交差するように矢印を引くことを考える.ただし,矢の向きは赤い頂点が左に,青い頂点が右にくるようにつける.(下図参照)
これによって,三角形分割の上にいくつかの矢印が描かれる.ひとつの三角形に着目すると,それに入ってくる矢印の数は $1$ つ以下で,それから出る矢印の数も $1$ つ以下である.$\triangle ABC$ の境界をまたぐ矢印は,辺 $AB$ 上にのみ存在しうる.さらに,$1$ 次元版のSpernerの補題のときの議論より,辺 $AB$ 上で外から内に入るような矢印が必ず存在する. そのような矢印を一つ選び.矢印を順にたどって三角形分割の中の三角形を次々に訪れると,矢印がそれ以上続かない三角形で止まるか,辺 $AB$ をまたいで外へ出るか,どちらかが起きる.
前者の場合は,矢印がそれ以上続かない三角形の $3$ 頂点は赤青緑となる.後者の場合は,辺 $AB$ 上で赤青の $2$ 色が割り当てられた隣接する $2$ 点組の数が必ず奇数であることから,辺 $AB$ 上で外から内に入るような別の矢印が存在する.したがって,前者の場合が必ず発生することが従う.
