平面上の $2$ つの円の位置関係の分類について解説します.
平面上に $2$ つの円があるとき,それらの位置関係は以下の $5$ つのパターンに分類されます.
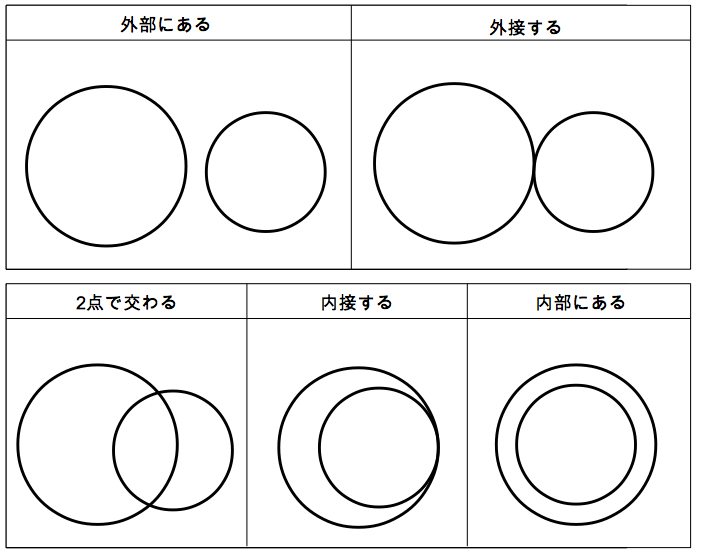
外部,内部にあるときは共有点は $0$ 個であり,内接,外接のときは共有点はちょうど $1$ 個であり, $2$ 点で交わるときは共有点は $2$ 個です.
さて,$2$ つの円の図が与えられれば,それらがどの位置関係にあるかは一目瞭然です.では,$2$ つの円の方程式が与えられたとき,それらの円の位置関係がどうなっているかを判定することはできるでしょうか.たとえば,円 $x^2+y^2=25$ と 円 $x^2-2x+y^2-4y-11=0$ の位置関係はどうなっているでしょうか.
以下では,この疑問に答えます.
結論から言えば,$2$ つの円の方程式からそれらの位置関係を判定することは可能であり,さらにその判定方法は簡単です. まず,簡単のために $2$ つの円の半径は相異なると仮定しておきます.大きい方の半径を $\color{red}{r_1}$,小さい方の半径を $\color{blue}{r_2}$ とおきます ($\color{red}{r_1} > \color{blue}{r_2}$) .さらに $2$ 円の中心間の距離を $d$ とおきます.このとき,$2$ つの円の位置関係は,$\color{red}{r_1},\color{blue}{r_2},d$ の関係式によって完全に分類することができます.
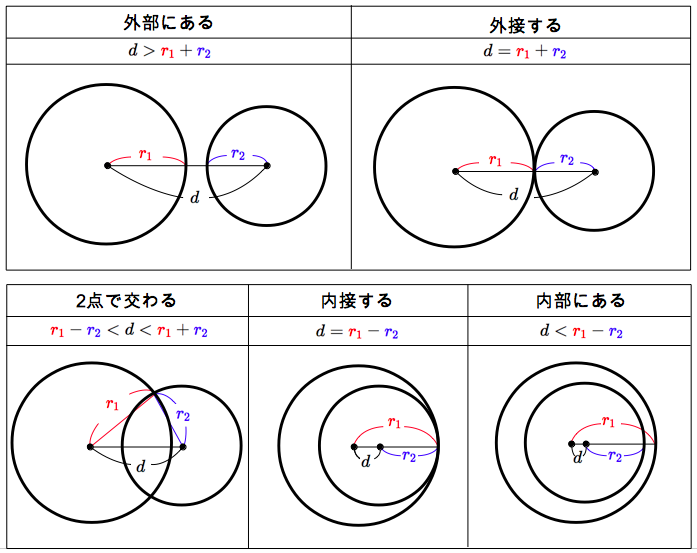
つまり,$2$ 円の方程式から,$d,r_1,r_2$ の値をそれぞれ計算し,それらが上の $5$ つのパターンのうち,どれにあてはまるかを考えれば,$2$ つの円の位置関係を知ることができます.方程式を用いて円の半径や中心間の距離を求めるという代数的な計算から,位置関係という幾何的な情報を得ることができるのです.
注意
・$r_1=r_2$ のときは,『内接する』場合と『内部にある』場合が起こり得ず,代わりに『一致する』という場合が起こり得ます.つまり,$d=r_1-r_2=0$ の場合のときに限り,$2$ 円は一致します.
・$2$ 円の半径の大小関係があらかじめわかっていないときは,上の関係式における $r_1-r_2$ のかわりに $|r_1-r_2|$ を用います.
上節でみたように,$2$ 円の位置関係を調べるには,$2$ つの円の半径と,中心間の距離を調べればよいのでした.円の方程式からその中心の座標と半径を求める方法は前記事 →円の方程式の表し方 で紹介しています.これらの知識を用いて,実際にいくつかの例題を解いてみましょう.
問 $2$ つの円 $x^2+y^2=25$ と $x^2-2x+y^2-4y-11=0$ の位置関係を求めよ.
$x^2+y^2=25$ の中心の座標は $(0,0)$,半径は $5$ です.また,$x^2-2x+y^2-4y-11=0$ を変形すると,$(x-1)^2+(y-2)^2=16$ となるので,中心の座標は $(1,2)$,半径は $4$ です.したがって,$2$ 円の中心間の距離は, $$\sqrt{(1-0)^2+(2-0)^2}=\sqrt{5}$$ と計算できます.$2$ 円の半径の和は $4+5=9$,$2$ 円の半径の差は $5-4=1$ したがって, $$1 < \text{(中心間の距離)}=\sqrt{5} < 9$$ が成り立ちます. よって,$2$ 円の位置関係は$2$ 点で交わる です.
問 中心が点 $(2,3)$ で,円 $x^2+y^2=16$ に内接する円の方程式を求めよ.
求める円の半径を $a$ とおきます.
$x^2+y^2=16$ の中心の座標は $(0,0)$,半径は $4$ です.したがって,$2$ 円の中心間の距離は $$\sqrt{(2-0)^2+(3-0)^2}=\sqrt{13}$$ です. 内接の条件より, $$4-a=\sqrt{13}$$ が成り立ちます. よって,$a=4-\sqrt{13}$.したがって求める円の方程式は $$(x-2)^2+(y-3)^2=(4-\sqrt{13})^2$$ です.
問 $2$ 円 $x^2+y^2=1,(x-a)^2+(y-2)^2=2$ が相異なる $2$ 点で交わるための $a$ の条件を求めよ.
$x^2+y^2=1$ の中心の座標は $(0,0)$,半径は $1$ です.
また,$(x-a)^2+(y-2)^2=2$ の中心の座標は $(a,2)$,半径は $2$ です.したがって,$2$ 円の中心間の距離は $$\sqrt{(a-0)^2+(2-0)^2}=\sqrt{a^2+4}$$ です.したがって,$2$ 円が相異なる $2$ 点で交わるための条件式は $$2-1 < \sqrt{a^2+4} < 2+1$$ です. ゆえに $1 < \sqrt{a^2+4} < 3$.これを解いて $-\sqrt{5} < a < \sqrt{5}$ を得ます.
問 $2$ つの円 $x^2+y^2=9$ と $x^2-6x+y^2+8y+21=0$ の位置関係を求めよ.
$x^2+y^2=9$ の中心の座標は $(0,0)$,半径は $3$ .
また,$x^2-6x+y^2+8y+21=0$ を変形すると,$(x-3)^2+(y+4)^2=4$ となるので,中心の座標は $(3,-4)$,半径は $2$.したがって,$2$ 円の中心間の距離は, $$\sqrt{(3-0)^2+(-4-0)^2}=5$$ と計算できる.$2$ 円の半径の和は $3+2=5$,$2$ 円の半径の差は $3-2=1$ したがって, $$\text{(中心間の距離)}= 5=\text{$2$ 円の半径の和}$$ なので,$2$ 円の位置関係は内接する.
問 中心が点 $(-1,7)$ で,円 $x^2+y^2-8x+10y+16=0$ に接する円の方程式を求めよ.
求める円の半径を $x$ とする.$x^2+y^2-8x+10y+16=0$ を変形すると,$(x-4)^2+(y-5)^2=25$ であるから,この円の中心は $(4,5)$ で半径は $5$ .したがって,$2$ 円の中心間の距離は $\sqrt{29}$. (i) 2円が外接するとき $\sqrt{29}=5+x$ より,$x=\sqrt{29}-5$ である. (ii) $x^2+y^2-8x+10y+16=0$ が求める円に内接するとき $\sqrt{29}=x-5$ より,$x=\sqrt{29}+5$ である.
以上 (i),(ii) より,求める円の方程式は $$(x+1)^2+(y-7)^2=(\sqrt{29}-5)^2$$ $$(x+1)^2+(y-7)^2=(\sqrt{29}+5)^2$$
問 $2$ つの円 $x^2+y^2=1$ と $(x-a)^2+y^2=\frac{a^2}{9} (a > 0)$ が相異なる $2$ 点で交わるとき,$a$ の値の範囲を求めよ.
$x^2+y^2=1$ の中心の座標は $(0,0)$,半径は $1$ .一方,$(x-a)^2+y^2=\frac{a^2}{9}$ の中心の座標は $(a,0)$,半径は $\frac{a}{3}$ .したがって,$2$ 円の中心間の距離は $a$.よって,$2$ 円が相異なる $2$ 点で交わるとき,つぎの関係式が成り立つ. $$\left | 1-\frac{a}{3} \right| < a < 1+\frac{a}{3}$$ $\left | 1-\frac{a}{3} \right| < a$ より,$\frac{3}{4} < a$ を得る. また,$a < 1+\frac{a}{3}$ より,$a < \frac{3}{2}$ を得る.
以上より,$\frac{3}{4} < a < \frac{3}{2}$ となる.