三角関数の分野で,最も基本的な定理のひとつが三角関数の加法定理です.三角関数の他の様々な公式が,加法定理から導くことができます.一見ややこしく見えますが,絶対に覚えるべき公式です.
三角関数の加法定理 ($\sin \cos$): $\alpha,\beta$ を実数とするとき,次が成り立つ. $$\large (1)\ \sin(\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta$$ $$\large (2)\ \sin(\alpha-\beta)=\sin\alpha \cos \beta-\cos \alpha\sin \beta$$ $$\large (3)\ \cos(\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha\sin \beta$$ $$\large (4)\ \cos(\alpha-\beta)=\cos \alpha\cos \beta+\sin \alpha\sin \beta$$
これら $4$ つの式のいずれも加法定理と呼ばれます.$\alpha,\beta$ は実数であれば,どのような値でも構いません.加法定理の最も簡単な応用は,細かい角度の正弦や余弦の値を求めることです.
例
$$・\sin \frac{5}{12}\pi=\sin \left(\frac{\pi}{4}+\frac{\pi}{6}\right)=\sin \frac{\pi}{4} \cos \frac{\pi}{6}+\cos \frac{\pi}{4}\sin \frac{\pi}{6}=\frac{\sqrt{2}}{2}\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$$ $$・\cos \frac{7}{12}\pi=\cos \left(\frac{\pi}{3}+\frac{\pi}{4} \right)=\cos \frac{\pi}{3}\cos \frac{\pi}{4}-\sin\frac{\pi}{3}\sin \frac{\pi}{4}=\frac{1}{2}\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}\frac{\sqrt{2}}{2}=\frac{\sqrt{2}-\sqrt{6}}{4}$$
上の公式と,$\tan \theta=\frac{\sin \theta}{\cos \theta}$ を用いれば,正接の加法定理の公式が導かれます.
三角関数の加法定理 ($\tan$): $$\large (1)\ \tan(\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha\tan \beta}$$ $$\large (2)\ \tan(\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha\tan \beta}$$
以下では主に正弦と余弦の加法定理の $(1)\ (3)$ についてのみ考察します.特に,加法定理を忘れてしまった場合に,その他の知識から復元するための方法をいくつか紹介します.
加法定理の厳密な証明は面倒なのでこの記事ではしません.その代わりに,加法定理を図形的に理解する方法を紹介します.
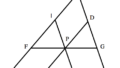
$\alpha >0,\beta > 0,0 < \alpha+\beta そして,これらを下のようにくっつけます.
さらに,下図のように補助線と座標を導入します.
上の図形において,点 $P$ の座標を $2$ 通りの方法で求めることで三角関数の加法定理を導きます. まず,三角比の定義を用いてすべての辺の長さを求めると,下図のようになります.
$P$ の $x$ 座標は, $$OC-HC=OC-AP=\cos \alpha\cos \beta-\sin\alpha\sin\beta$$ です.また,$P$ の $y$ 座標は, $$PH=AB+BC=\sin \alpha\sin \beta+\cos \alpha\cos \beta$$ です.一方,$△POH$ に注目すると,$\angle POH=\alpha+\beta$ より,$P$ の $x$ 座標は $\cos (\alpha+\beta)$,$y$ 座標は $\sin (\alpha+\beta)$ です. 以上より, $$\sin(\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta$$ $$\cos(\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha\sin \beta$$ が導かれます.
この図形的考察は,$\alpha$ や $\beta$ のとりうる範囲に制限があるので,一般の加法定理についての証明にはなっていません.しかし,たとえば加法定理をど忘れてしまった場合などにこの図形を覚えていれば,簡単に復元することができます.
複素指数関数の指数法則は加法定理から導かれます.逆に,指数法則を覚えていれば,加法定理を簡単に復元できます.
複素指数関数の指数法則: $z_1,z_2$ を複素数とするとき, $$\large e^{z_1+z_2}=e^{z_1}e^{z_2}$$ が成り立つ.
特に,$\alpha,\beta$ を実数とすると, $$e^{i(\alpha+\beta)}=e^{i\alpha}e^{i\beta}$$ が成り立ちます. この式において,(左辺) = $\cos(\alpha+\beta)+i \sin(\alpha+\beta)$ です.
一方,$$(右辺) = (\cos \alpha+i \sin \alpha)(\cos \beta+i\sin \beta)=(\cos \alpha\cos \beta-\sin \alpha\sin \beta)+i(\sin \alpha\cos \beta+\cos \alpha\sin \beta)$$ です. したがって,実部と虚部を比較すると, $$\sin(\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta$$ $$\cos(\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha\sin \beta$$ が得られます.
回転行列 (回転移動の表現行列) は加法定理から導かれます.逆に,回転行列を覚えていれば,加法定理を簡単に復元できます.
原点周りの回転移動: 座標平面上の点を原点周りに $\theta$ だけ回転させる一次変換を表す行列は, $$\left( \begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right)$$ である.
原点周りに $\alpha,\beta$ 回転させる一次変換をそれぞれ $f,g$ とし,それらの表現行列を $A,B$ とします.
$g\circ f$ は原点周りに $\alpha+\beta$ 回転させる一次変換を表すので,この表現行列は, $$\left( \begin{array}{rr} \cos (\alpha+\beta) & -\sin (\alpha+\beta) \\ \sin (\alpha+\beta) & \cos (\alpha+\beta) \end{array} \right)$$ です.一方, $$BA=\left( \begin{array}{rr} \cos \beta & -\sin \beta \\ \sin \beta & \cos \beta \end{array} \right)\left( \begin{array}{rr} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array} \right) =\left( \begin{array}{rr} \cos \alpha \cos \beta-\sin \alpha\sin \beta &-\sin \alpha\cos \beta-\cos \alpha\sin \beta\\ \sin \alpha\cos \beta+\cos \alpha\sin \beta&\cos \alpha \cos \beta-\sin \alpha\sin \beta \end{array} \right)$$ これらの行列の各成分を比較すると, $$\sin(\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta$$ $$\cos(\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha\sin \beta$$ が得られます.