三角形の面積のいろいろな表し方についてまとめました．
底辺を $x$， 高さを $y$ とすると，三角形の面積 $S$ は次のように表せる． $$\large S=\frac{1}{2}xy$$
おそらく一番最初に習う三角形の面積の公式です．
この公式は説明不要ですね．どんどんステップアップしていきましょう．
$3$ 点 $O(0,0),P(a,b),Q(c,d)$ を頂点とする三角形の面積 $S$ は次のように表せる． $$\large S=\frac{1}{2}|ad-bc|$$
$3$ 点の座標が与えられたとき，その三角形の面積を，座標の成分を用いて表す公式です．この公式は，たとえば，直線 $OP$ の方程式を求め，点 $Q$ と 直線 $OP$ の距離を求めるなどすれば導けます． また，一般に $3$ 点 $A(a_1,a_2),B(b_1,b_2),C(c_1,c_2)$ が与えられた場合には，$1$ 点が原点に来るように平行移動して，$A'(0,0),B'(b_1-a_1,b_2-a_2),C'(c_1-a_1,c_2-a_2)$ を考えれば，$3$ 点 $A,B,C$ を頂点とする三角形の面積がわかります．
三角形 $2$ 辺を $a,b$ その間の角を $\theta$ とすると，三角形の面積 $S$ は次のように表せる． $$\large S=\frac{1}{2}ab \sin \theta$$
三角形の一辺 $a$ を底辺と考えると，その高さは $b\sin \theta$ となります．したがって，(底辺)×(高さ)÷2 の公式を用いればこの公式が導けます． $\theta$ は $2$ 辺 $a,b$ で挟まれた角でなければならないことに注意してください．
非常によく用いられる重要度の高い公式です．
$2$ つのベクトル $\vec{a},\vec{b}$ で張られる三角形の面積 $S$ は次のように表せる． $$\large S=\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}$$
$2$ つのべクトルの長さと内積を用いた三角形の面積の公式です．
この公式は， $\sin \theta=\sqrt{1-\cos^2 \theta}$ と， $|\vec{a}||\vec{b}|\cos \theta=\vec{a}\cdot\vec{b}$ を用いれば，前の公式 $ S=\frac{1}{2}ab \sin \theta$ より導くことができます．
三角形の $3$ 辺を $a,b,c$とし，$s=\frac{1}{2}(a+b+c)$ とすると，三角形の面積 $S$ は次のように表せる． $$\large S=\sqrt{s(s-a)(s-b)(s-c)}$$
$3$ 辺の長さが与えられたときに三角形の面積を求める公式です．
この公式は非常に美しいですが，必ずしも覚える必要はありません (もちろん覚えてしまってもよいですが).なぜなら，三角形の $3$ 辺が与えられれば，余弦定理よりひとつの角の余弦がわかります．そこから正弦を求めて，公式 $ S=\frac{1}{2}ab \sin \theta$ を用いれば，三角形の面積が求められるからです．
頻繁に余弦定理の練習を積まされているであろう高校生にとっては，ヘロンの公式を用いるより上で述べた方法の方が早い気がします．
三角形の $3$ 辺を $a,b,c$とし，内接円の半径を$r$ とすると，三角形の面積 $S$ は次のように表せる． $$\large S=\frac{1}{2}r(a+b+c)$$
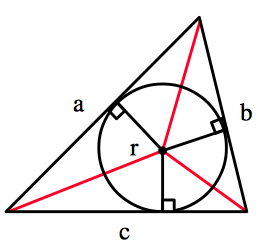内接円の半径がわかっていないと使えないので，使える状況が限定的ですが，覚えておきたい公式です． この公式は，右図のように三角形を $3$ つに分割して，それぞれの三角形の面積を足すことにより導けます．
逆に，三角形の面積と，$3$ 辺の長さがわかっていると，内接円の半径が求められます．
三角形の $3$ 辺を $a,b,c$とし，外接円の半径を $R$ とすると，三角形の面積 $S$ は次のように表せる． $$S=\frac{abc}{4R}$$
$3$ 辺の長さと外接円の半径を用いて三角形の面積を表すこともできます．
この公式は，正弦定理 $$\frac{c}{\sin C}=2R$$ を上の方の節で紹介した $S=\frac{1}{2}ab \sin C$ に代入すれば導かれます．ただし，上の節での $\theta$ はここでは，$C$ のことです．
導き方からわかるように，有名定理と，有名な公式を用いればすぐに導き出せるので，覚える必要はありません．マイナーな公式をたくさん覚えるよりも，重要な公式や定理を臨機応変に使えるようになる方が大切です．
状況に応じで公式・定理を使い分けることが重要ですね．
