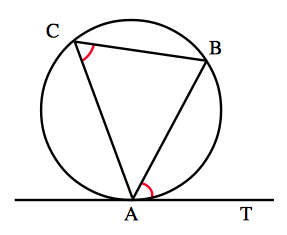
接弦定理: 円 $O$ の弦 $AB$ と,点 $A$ における接線 $AT$ とのなす角 $\angle BAT$ は,その角の内部に含まれる弧 $AB$ に対する円周角 $\angle ACB$ に等しい.
一般に,円 $O$ とその円の弦 $AB$ があるとき,弧 $AB$ というのは,$2$ 種類考えられます.(下図の赤い部分と青い部分) それに伴って,弧 $AB$ の円周角も $2$ 種類考えられます.
接弦定理の主張の中で,単に「弧 $AB$ に対する円周角 $\angle ACB$」と述べずに,「〜の内部に含まれる弧 $AB$ に対する円周角 $\angle ACB$ 」と述べているのは,この曖昧さをなくすためです.
標準的な教科書に載っているものではない証明を載せておきます.別証明というほど大したものではありませんが,以下のように示すこともできます.
接弦定理の証明:
Case1: $\angle BAT$ が直角の場合 この場合,線分 $AB$ は円 $O$ の直径になる.したがって,$\angle ACB=\frac{\pi}{2}$ となって,$\angle ACB=\angle BAT.$
Case2: $\angle BAT$ が鋭角の場合 $\angle BAT=\alpha$ とすると, $\angle OAB=\frac{\pi}{2}-\alpha$ で,$△OAB$ は二等辺三角形なので,$\angle AOB=2\alpha.$ 円周角と中心角の関係より,$\angle ACB=\alpha.$ したがって,$\angle ACB=\angle BAT.$
Case3: $\angle BAT$ が鈍角の場合 $\angle BAT=\alpha$ とすると,$\angle OAB=\alpha-\frac{\pi}{2}$ で,$△OAB$ は二等辺三角形なので,$\angle AOB=2\pi-2\alpha.$ これより,$\angle ACB=\alpha$ となる.したがって,$\angle ACB=\angle BAT.$
よって,いずれの場合にも $\angle ACB=\angle BAT$ が成り立つ.
マイナーですが,接弦定理はその逆の主張も成り立ちます.
接弦定理の逆: 円 $O$ の弧 $AB$ と半直線 $AT$ が直線 $AB$ の同じ側にあって,弧 $AB$ に対する円周角の $\angle ACB$ が,$\angle BAT$ と等しいとき,直線 $AT$ は点 $A$ における円 $O$ の接線である.

接弦定理の逆の証明: 点 $A$ を通る円 $O$ の接線上に,点 $T’$ を,$\angle BAT’$ が弧 $AB$ を含むようにとる.このとき,接弦定理より, $$\angle ACB=\angle BAT’$$ である.また仮定から, $$\angle ACB=\angle BAT$$ なので,$\angle BAT’=\angle BAT$ となる.したがって,直線 $AT$ と直線 $AT’$ は一致する.よって,直線 $AT$ は点 $A$ における円 $O$ の接線である.
問 $△ABC$ とその外接円 $O$ について,円 $O$ の $A$ における接線と,$B$ における接線の交点を $P$ とする.$P$ を通り,線分 $AC$ に平行な直線と線分 $BC$ との交点を $D$ とする.$AD=CD$ を示せ.
問 円に内接する四角形 $ABCD$ について,$AC$ と $BD$ の交点を $P$ とする.また,$P$ を通り線分 $AB$ に平行な直線を $l$ とする.直線 $l$ は,$△PCD$ の外接円に点 $P$ で接することを示せ.