下図に数の種類をまとめました.ややこしくなるのを避けるために $2$ つに分けています.
実数は有理数と無理数のふたつにわけられます.小数で表したとき,有限でとまるか,循環するものが,有理数で,循環せずに無限につづくものが無理数です.
さらに,有理数は整数という特別な数を含みます.
整数のうち,正の数を自然数とよびます.(ただし,$0$ を自然数に含める流儀もあります.) 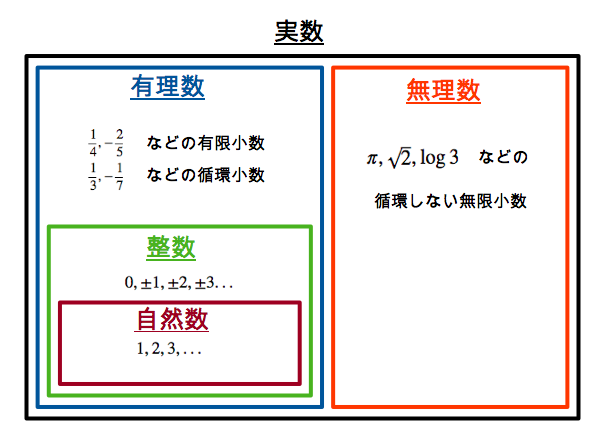
$i$ は虚数単位で,$2$ 乗すると $-1$ となる数です.
特に複素数,虚数,純虚数の違いが間違いやすいでので気をつけてください.虚数は実数でない複素数のことです.純虚数は,実部が $0$ の虚数のことです.今回は実数に含まれる数についてその特徴を紹介します.複素数については別の記事で扱います.
自然数とは $1,2,3,…$ と続く数のことです.$0$ を自然数に含める流儀もありますが,日本の初等教育では $0$ を自然数に含めないことになっています.これはほとんど好みの問題です.自然数の重要な特徴のひとつは, 自然数からなる空でない集合は最小元をもつというものです.たとえば,素数全体の集合は最小元 $2$ を持ちます.言われてみればこの事実は当たり前のことと思うかもしれませんが,このような基本的な事柄が決め手となって解決する問題も多くあります.
自然数全体の集合は加法について閉じています.つまり,$2$ つの自然数を足した数は必ず自然数になります.しかし,それ以外の演算 (減法,乗法,除法) については閉じていません.
整数とは $0,\pm{1},\pm{2},\pm{3},…$と続く数のことです.整数の重要な特徴のひとつは,除法の原理が成り立つことです.除法の原理とは次のようなものです.
除法の原理: $2$ つの整数 $a,b (b \neq 0)$ に対して, $$a=bq+r (0 \le r < |b|)$$ を満たす整数 $q,r$ が一意的に存在する.
簡単にいうと,割り算の概念があるということです.
また,どの $2$ つの整数の差の絶対値も $1$ 以上であるという性質も重要です.つまり,$a$ を整数とすると,開区間 $(a-1,a+1)$ には整数は含まれていません.これは当然のことですが,イメージで言えば,数直線上で整数は点々と(ポツポツと)存在しているという感じです.
整数全体の集合は加法・減法・乗法について閉じています. しかし,除法については閉じていません.
有理数とは,整数 $m,n (n \neq 0)$ を用いて,分数 $\frac{m}{n}$ の形で表される数のことです.整数も当然有理数です($n$ が $m$ の約数のとき,$\frac{m}{n}$ は整数).有理数は $2$ つの数の比を表していると考えることができます.
有理数はさらに整数と有限小数と循環小数にわけられます. 有理数の最も重要な特徴のひとつは,稠密性 (ちゅうみつせい)が成り立つことです.これは,$2$ つの有理数の間には必ず別の有理数が存在するということです.実際に,$a,b$ を$2$ つの有理数とすると, $$a
有理数全体の集合は加法・減法・乗法・除法すべての演算について閉じています.
実数とは,整数と,有限小数または無限小数で表される数のことです.実数の最も重要な特徴のひとつは,連続性が成り立つことですが,このことをきちんと説明するには厳密な数学の準備が必要ですので,ここでは深く立ち入らないことにします.
実数全体の集合は加法・減法・乗法・除法すべての演算について閉じています.
無理数とは,有理数でない実数のことです.$\pi,\sqrt{2}$ や,自然対数の低 $e$ などが代表的な無理数です.さて,ここまで様々な数の集合に関して演算でどこまで閉じているかを紹介してきましたが,無理数同士の演算はろくなことが言えません.その意味で無理数の集合は例外的です.たとえば,$\sqrt{2}+(-\sqrt{2})=0$ で,$0$ は無理数ではないので,無理数の集合は加法(減法)について閉じていません.また,$\sqrt{2} \times \sqrt{2}=2$ で,$2$ は無理数ではないので,乗法についても閉じていません.同様に除法についても閉じていません.さらに, $$(無理数)^{(無理数)}$$ すなわち無理数の無理数乗が無理数かどうか,という問題はどうでしょうか.これはたとえば, $$e^{log3}=3, e^{log\sqrt{3}}=\sqrt{3}$$ などを考えると,有理数にも無理数にもなりうる.ということになります.
さて,種々の演算についてどこまで閉じているか,という問題に関して,無理数だけ異質であることを見てきましたが,これはどうしてでしょうか.そのひとつの回答は,はじめの図にあります.この図を再度見て何か気づくことはないでしょうか.図をみると整数,有理数,実数,複素数はすべて自然数の拡張と考えることができます.気分的に言えば,演算について閉じるという性質は集合の範囲が増えればより成り立ちやすくなりそうです.実際,有理数まで範囲を広げれば加減乗除すべての演算で閉じます.ところが無理数はある体系を拡張したようなものではありません.いわばあまりもの全体を無理数と名付けた感じです.このことが起因しているといえるでしょう.
複素数については紹介するべきことが多すぎるので,別の記事に書くことにします.
