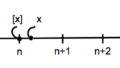
正十一角形の頂点を $3$ 色の色 赤,青,緑に彩色します.ただし,赤色の頂点の個数は奇数個,青色の頂点の個数も奇数個,緑色の頂点の個数も奇数個となるようにします.たとえば,下図はそのような彩色の例です.
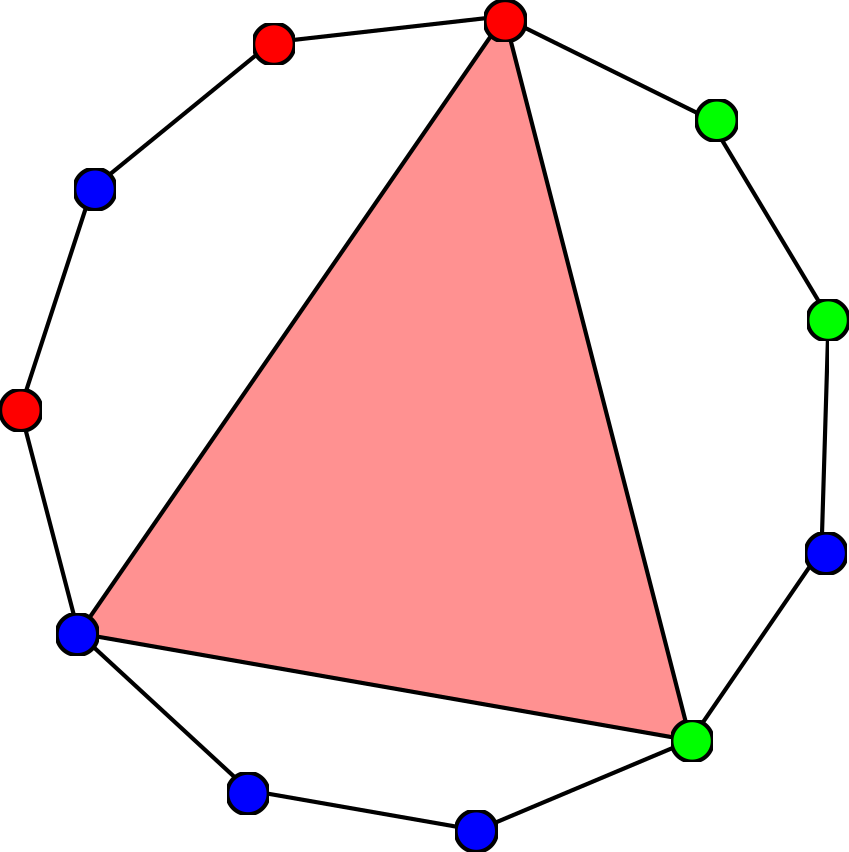
このとき,図のように,$3$ 頂点に割り当てられた色が相異なるような二等辺三角形が必ず存在します.この彩色の例では条件を満たすような二等辺三角形は他にもあります.条件を満たすようなどのような彩色に対しても,$3$ 頂点に割り当てられた色が相異なるような二等辺三角形が少なくともひとつは存在することを示す問題です.
このように,彩色+存在(または不存在の)証明は組合せ数学の問題ではありがちですが,その中でもかなり難しめの問題だと思います.いろいろな観点から考察する必要があります.上級者向けの問題であることを注意しておきます.
ヒント
実はこの主張は,正七角形でも同様に成り立ちます.
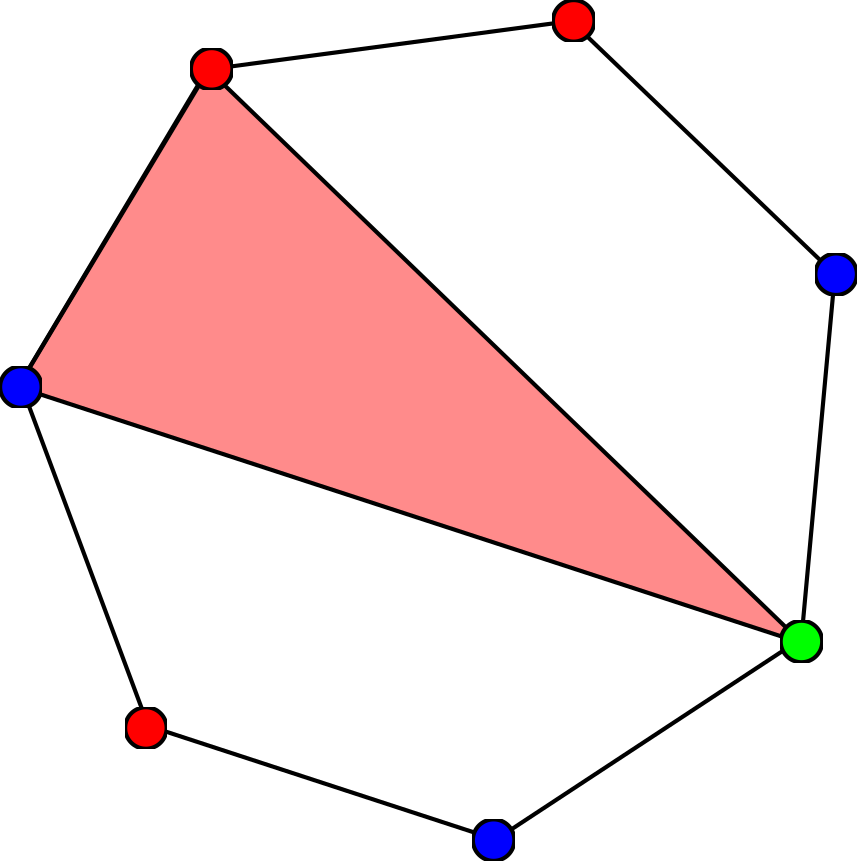
本問題の前に正七角形の場合で考察すると,何か手がかりが得られるかもしれません.
ヒント
まず手始めに,正十一角形の頂点から $3$ つの頂点を選んでつくられる三角形について考えてみましょう.以下では,三角形といえば,正十一角形の頂点から $3$ つの頂点を選んでつくられる三角形についてのみ言及していることに注意してください.簡単な観察により次が従います.(各自確認してみてください)
観察 $1$ 正十一角形の頂点から $3$ つの頂点を選んでつくられる三角形は正三角形にはならない.
観察 $2$ 正十一角形の頂点から $2$ つの頂点を選ぶと,それらを結ぶ線分を底辺とする二等辺三角形がただひとつ決まる.
観察 $1,2$ から二等辺三角形の個数がわかります.
観察 $3$ 正十一角形の頂点から $3$ つの頂点を選んでつくられる二等辺三角形の数は ${}_{11} \mathrm{C} _2$ 個ある.
一方,以下のことも確かめられます.
観察 $4$ 正十一角形の頂点から $2$ つの頂点を選ぶと,それらを結ぶ線分を含む二等辺三角形はちょうど $3$ つある.
解答例
背理法で示します.すなわち,$3$ 頂点に割り当てられた色が相異なるような二等辺三角形が存在しないと仮定して,矛盾を導きます.
赤頂点の個数を $a$, 青頂点の個数を $b$, 緑頂点の個数を $c$ とします.
正十一角形の頂点から $3$ つの頂点を選んでつくられる二等辺三角形全体を考えます.仮定より,二等辺三角形は『すべての頂点が同色』か,『$2$ 点が同じ色で,残りの $1$ 点が異なる色』であるような $2$ つのパターンに分けられます. すべての頂点が同色であるような二等辺三角形の個数を $x$ とし,$2$ 色が同じ色で,残りの $1$ 色が異なる色であるような二等辺三角形の個数を $y$ とします. 観察 $3$ から,$x+y= {}_{11} \mathrm{C} _2$ となります.
二等辺三角形全体に対して,両端点が同色であるような辺の数の総和 $A$ を $2$ 通りの方法で数え上げることを考えます.
まず,二等辺三角形のすべての頂点が同色のとき,両端点が同色の辺は $3$ つあります.また,$2$ 色が同じ色で,残りの $1$ 色が異なる色であるような二等辺三角形について,両端点が同色の辺は $1$ つあります.したがって, $$A=y+3x$$ が成り立ちます.
一方,観察 $4$ より,同色の $2$ 点を任意に固定すると,その辺を含む二等辺三角形はちょうど $3$ つあります.また,同色の $2$ 点を選ぶ方法は ${}_a \mathrm{C} _2+{}_b \mathrm{C} _2+{}_c \mathrm{C} _2$ 通りあります.したがって, $$A = 3({}_a \mathrm{C} _2+{}_b \mathrm{C} _2+{}_c \mathrm{C} _2)$$ が成り立ちます.よって, $$y+3x=3({}_a \mathrm{C} _2+{}_b \mathrm{C} _2+{}_c \mathrm{C} _2)$$ となり,$x+y= {}_{11} \mathrm{C} _2$ を用いると, $${}_{11} \mathrm{C} _2 +2Y = 3({}_a \mathrm{C} _2+{}_b \mathrm{C} _2+{}_c \mathrm{C} _2)$$ が従います.ここで,左辺と右辺の偶奇に着目すると, $${}_{11} \mathrm{C} _2 \equiv {}_a \mathrm{C} _2+{}_b \mathrm{C} _2+{}_c \mathrm{C} _2 \ \ (\mathrm{mod}\ 2)$$ となります.したがって, $$11^2-11 \equiv a^2-a + b^2-b + c^2-c \ \ (\mathrm{mod}\ 4)$$ となりますが,$a+b+c=11$ なので, $$11^2 \equiv a^2+b^2+c^2\ \ (\mathrm{mod}\ 4)$$ です.ところが仮定から $a,b,c$ はすべて奇数だったので,$a^2 \equiv 1, b^2 \equiv 1, c^2 \equiv 1 \ \ (\mathrm{mod}\ 4)$ であるから, $$11^2 \equiv 3\ \ (\mathrm{mod}\ 4)$$ となりますが,これは矛盾です.($11^2$ を $4$ で割ったあまりは $3$ にならないので)
以上より,題意が示されました.