マイナーですが,正七角形の辺と対角線に関する美しい公式です.
トレミーの定理を知っている人は,この問題はとても簡単かもしれません.ここでは,$2$ 通りの解答を紹介します.
三角比を用いる解答例
三辺が $a,b,c$ の三角形の内角に注目すると,それぞれの角度が $\frac{\pi}{7},\frac{2\pi}{7},\frac{4\pi}{7}$ であることが容易にわかります.
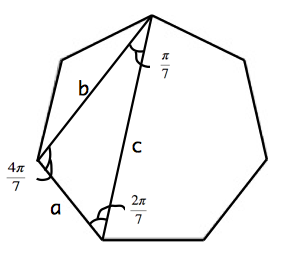
したがって,正弦定理より, $$\frac{\sin \left( \frac{\pi}{7} \right)}{a}=\frac{\sin \left( \frac{2\pi}{7} \right)}{b}=\frac{\sin \left(\frac{4\pi}{7} \right)}{c}=\frac{1}{2R}$$ であることがわかります.ここで,$R$ はこの三角形の外接円の半径です. すると, $$\frac{1}{b}+\frac{1}{c}=\frac{1}{2R}\left( \frac{1}{\sin \left( \frac{2\pi}{7} \right)}+\frac{1}{\sin \left( \frac{4\pi}{7} \right)} \right) \\ =\frac{\sin \left( \frac{\pi}{7} \right)}{a}\left( \frac{1}{\sin \left( \frac{2\pi}{7} \right)}+\frac{1}{\sin \left( \frac{4\pi}{7} \right)} \right)$$ となるので,$$\sin \left( \frac{\pi}{7} \right)\left( \frac{1}{\sin \left( \frac{2\pi}{7} \right)}+\frac{1}{\sin \left( \frac{4\pi}{7} \right)} \right)=1$$ を示せばよいです.倍角公式や,和積公式を用いると, $$\sin \left( \frac{\pi}{7} \right)\left( \frac{1}{\sin \left( \frac{2\pi}{7} \right)}+\frac{1}{\sin \left( \frac{4\pi}{7} \right)} \right)=\sin \left( \frac{\pi}{7} \right) \left( \frac{\sin \left( \frac{4\pi}{7} \right)+\sin \left( \frac{2\pi}{7} \right)}{\sin \left( \frac{2\pi}{7} \right)\sin \left( \frac{4\pi}{7} \right)} \right) \\ =\frac{\sin \left( \frac{4\pi}{7} \right)+\sin \left( \frac{2\pi}{7} \right)}{2 \cos \left(\frac{\pi}{7} \right) \sin \left( \frac{4\pi}{7} \right)} \\ =\frac{2 \sin \left(\frac{3\pi}{7} \right) \cos \left( \frac{\pi}{7} \right)}{2 \cos \left(\frac{\pi}{7} \right) \sin \left( \frac{4\pi}{7} \right)}=1$$ となります ($\sin \left( \frac{3\pi}{7} \right)=\sin \left( \frac{4\pi}{7} \right)$ に注意してください).したがって, $$\frac{1}{a}=\frac{1}{b}+\frac{1}{c}$$ が成り立ちます.
トレミーの定理を用いる解答例
実は,この問題はトレミーの定理を用いるといとも簡単に解けてしまいます.
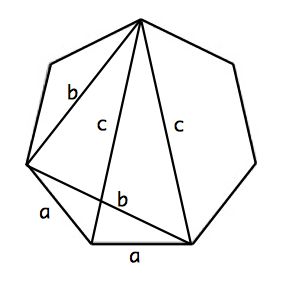
上図のように,補助線を引きます.正七角形は当然,円に内接しているので,トレミーの定理より, $$bc=ac+ab$$ が成り立ちます.両辺に $\frac{1}{abc}$ をかけると, $$\frac{1}{a}=\frac{1}{b}+\frac{1}{c}$$ となります.
調和のとれた美しい式ですね.
