解析学の広い範囲で極めて有用な絶対不等式である,Jensenの不等式について紹介します.
Jensenの不等式を説明する前の準備として,まずは凸関数とは何かを説明します.
凸関数の定義: 関数 $f(x)$ が凸関数であるとは,任意の $x,y$ および $0\le t\le 1$ を満たす任意の実数 $t$ に対して, $$tf(x)+(1-t)f(y)\ge f(tx+(1-t)y)$$ が成り立つことである.
任意の $x,y$ というのは当然,関数 $f$ の定義域内の任意の $x,y$ という意味です.
凸関数の図形的意味
凸関数は図形的にはへこんでいない関数というイメージです.このイメージを理解することが重要です. まず,左辺は $f(x)$ と $f(y)$ を $t:1-t$ に内分した値であり,右辺は $x$ と $y$ を $t:1-t$ に内分した値を $f$ で写したものだということに注意してください.これは下図のような状況を意味しています.
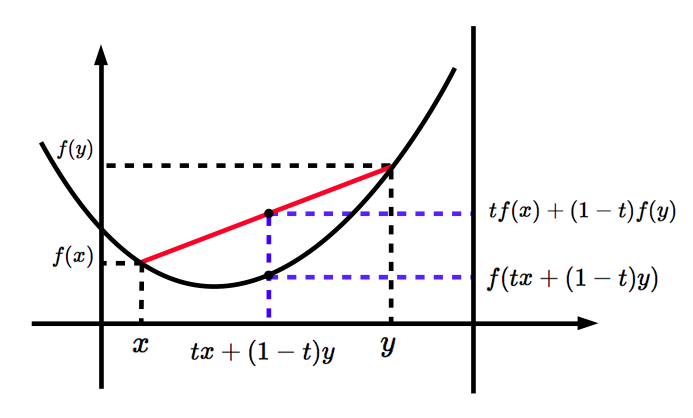
つまり,言い換えると,$y=f(x)$ が凸関数であるとは,『どのような $x,y$ を選んだとしても,$x$ と $y$ の間の区間においては,$(x,f(x))$ と$(y,f(y))$ を結ぶ線分は常に $y=f(x)$ より上側にある.』ということです.
凸関数の例
・$y=x (x\in \mathbb{R})$ ・$y=x^2 (x\in \mathbb{R})$ ・$y=e^x (x\in \mathbb{R})$ ・$y=e^{-x} (x\in \mathbb{R})$ ・$y=-\log x (x > 0)$
・$y=\sin x (\pi \le x\le 2\pi)$
Jensenの不等式とは,凸関数に対して成り立つつぎの不等式のことをいいます.この不等式はやや抽象的ですが,その分,非常に有用で汎用性が高く,他の様々な絶対不等式と関連しています.
Jensenの不等式: 関数 $f(x)$ を凸関数,$\alpha_1,…,\alpha_n$ を $\displaystyle \sum_{i=1}^n \alpha_i =1$ を満たす $n$ 個の正の実数とするとき,つぎの不等式が成り立つ. $$\large \sum_{i=1}^n \alpha_if(x_i)\ge f\left(\sum_{i=1}^n \alpha_ix_i\right)$$
・$\alpha_i$ は定数で,$x_i$ は変数です.
・$n=2$ のときは凸関数の定義 $tf(x)+(1-t)f(y)\ge f(tx+(1-t)y)$ に他なりません.したがって,Jensenの不等式は凸関数の定義を一般化させたものととらえることができます.
例
・$y=x^2$ に $n=2$,$\alpha_1=\frac{1}{4},\alpha_2=\frac{3}{4}$ として,適用すると, $$\frac{x^2+3y^2}{4}\ge \left(\frac{x+3y}{4}\right)^2$$ ・$y=e^x$ に $n=3$ ,$\alpha_1=\alpha_2=\alpha_3=\frac{1}{3}$ として,適用すると, $$\frac{e^{x}+e^{y}+e^{z}}{3}\ge e^{\left(\frac{x+y+z}{3}\right)}$$
数学的帰納法を使えばJensenの不等式を示すことができます.
証明:(数学的帰納法) $n=1$ のとき,示すべき不等式は $f(x)\ge f(x)$ となり,これは自明に成り立つ. $n=2$ のとき,示すべき不等式は $\alpha_1f(x_1)+\alpha_2f(x_2)\ge f(\alpha_1x_1+\alpha_2x_2)$ となるが,$\alpha_1+\alpha_2=1$ なので,これを不等式に代入して,$\alpha_2$ を消去すると, $$\alpha_1f(x_1)+(1-\alpha_1)f(x_2)\ge f(\alpha_1x_1+(1-\alpha_1)x_2)$$ となり,これは凸関数の性質そのものであるから,成り立つ. $n=k$ のとき,Jensenの不等式が成り立つと仮定する.
$n=k+1$ のとき, $$\sum_{i=1}^{k+1}\alpha_if(x_i)=\sum_{i=1}^{k} \alpha_if(x_i)+\alpha_{k+1}f(x_{k+1})$$ $$=\beta\sum_{i=1}^{k}\frac{\alpha_i}{\beta}f(x_i)+\alpha_{k+1}f(x_{k+1}) (\text{ただし}\beta=\sum_{i=1}^k \alpha_i \text{とおいた})$$ $$\ge \beta f\left(\sum_{i=1}^{k} \frac{\alpha_i}{\beta}x_i \right)+\alpha_{k+1}f(x_{k+1}) (\text{帰納法の仮定より})$$ $$\ge f\left(\sum_{i=1}^{k} \alpha_ix_i+\alpha_{k+1}x_{k+1}\right) (\text{凸関数の性質より})$$ $$=f\left(\sum_{i=1}^{k+1} \alpha_ix_i\right)$$ よって,数学的帰納法より,Jensenの不等式が示された.
$$\sum_{i=1}^{k+1}\alpha_if(x_i)=\sum_{i=1}^{k} \alpha_if(x_i)+\alpha_{k+1}f(x_{k+1})$$ は帰納法の仮定を使おうと思ったら自然に行う式変形です.右辺の第1項に対して,帰納法の仮定を用いたいのですが,このままでは,$\sum_{i=1}^{k} \alpha_i\neq 1$ なので,帰納法の仮定が使えません.そこで係数の和が $1$ となるように,各係数を $\frac{1}{\beta}$ 倍することで調整しています.そして,$\sum_{i=1}^{k}\frac{\alpha_i}{\beta}f(x_i)$ に対して帰納法の仮定を用います.
あとは,$\beta+\alpha_{k+1}=1$ であり,$f$ が凸関数であることの性質を用いればよいです.
問 $x,y,z$ を正の実数とするとき,つぎの不等式を示せ. $$\frac{x+y+z}{3}\ge \sqrt[3]{xyz}$$
$y=-\log x$ に $n=3,\alpha_i=\frac{1}{3}$ として,Jensenの不等式を適用すると, $$-\frac{\log xyz}{3}\ge -\log \frac{x+y+z}{3}$$ したがって, $$\log \frac{x+y+z}{3}\ge \log (xyz)^{\frac{1}{3}}$$ 底は $1$ より大きいので, $$\frac{x+y+z}{3}\ge \sqrt[3]{xyz}$$ となる.
問 $p>1$,$a,b$ を正の実数とするとき, つぎの不等式を示せ. $$2^{p-1}(a^p+b^p)\ge (a+b)^p$$
$y=x^p$ に $n=2,\alpha_i=\frac{1}{2}$ として,Jensenの不等式を適用すると, $$\frac{a^p+b^p}{2}\ge \left(\frac{a+b}{2}\right)^p$$ したがって, $$2^{p-1}(a^p+b^p)\ge (a+b)^p$$ となる.
問 $\alpha,\beta,\gamma$ は $\alpha>0,\beta> 0,\gamma> 0,\alpha+\beta+\gamma=\pi$ を満たすとする.このとき,$\sin \alpha\sin \beta\sin \gamma$ の最大値を求めよ.
$y=-\log \sin x$ に $n=3,\alpha_i=\frac{1}{3}$ として,Jensenの不等式を適用すると, $$-\frac{\log (\sin \alpha\sin \beta \sin \gamma)}{3}\ge -\log \sin \left(\frac{\alpha+\beta+\gamma}{3}\right)=-\log \sin \frac{\pi}{3}=-\log \frac{\sqrt{3}}{2}$$ したがって, $$\log (\sin \alpha\sin \beta \sin \gamma) \le 3\log \frac{\sqrt{3}}{2}$$ よって, $$\sin \alpha\sin \beta \sin \gamma\le \frac{3\sqrt{3}}{8}$$ 等号は $\alpha=\beta=\gamma=\frac{\pi}{3}$ のとき成立.
