$X$ を集合とします．$X$ の $n$ 個の部分集合の一般的な状況について，そのベン図による表し方を考えてみましょう．
ベン図 (venn diagram)とは，複数の集合の関係を平面上に視覚的に表したものです．
ベン図を用いることで，考察している集合同士の関係を明快に，そして直感的に理解することができます．
$X$ を集合とします．$A,B$ を $X$ の部分集合とするとき，この状況はベン図を用いて下図のように表すことができます．
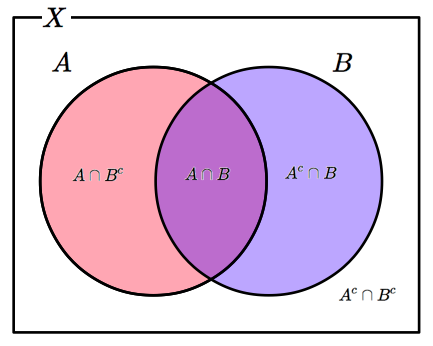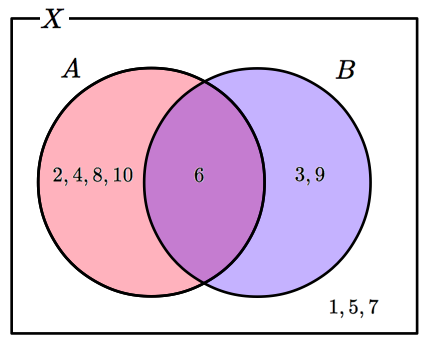
赤い円が集合 $A$ を表しており，青い円が集合 $B$ を表しています． たとえば，$X=\{1,2,3,4,5,6,7,8,9,10\}$，$A=\{2,4,6,8,10\}$，$B=\{3,6,9\}$ とするとき，これらの集合とその要素の関係は下図のようになります．
$n=3$
$X$ の部分集合が $A,B,C$ の $3$ つである場合は，ベン図は下図のようになります．
実用性の観点からいえば，$X$ の部分集合が $2$ つや $3$ つの場合のベン図を考えることがほとんどですが，$4$ つ以上の場合を考えてみましょう． 実は，$4$ つ以上の集合をすべて円で表すとすると，この状況をベン図で表現することは不可能であることが証明できます．
$n\ge 4$ とし，$A_1,…,A_n$ を $X$ の部分集合とします．$X$ の要素は $A_1$ に属すか属さないかの $2$ 通りあり，$A_2$ に属すか属さないかの $2$ 通りあり・・・，というように考えていくと，$2^n$ 通りのパターンがあります．つまり，この状況をベン図で表すためには，平面を $n$ 個の円で $2^n$ 個の領域に分割しなければなりません． これが不可能であることを証明しましょう．
$k$ 個 $(k\ge1)$ の円は，どのふたつもちょうど $2$ 点で交わり，どの $3$ つも共有点をもたないと仮定します．このとき，$k$ 個の円が分割する領域の個数を $a_k$ とおき，数列 $a_k$ に関する漸化式をたてます． $k=1$ のとき，明らかにひとつの円は平面を $2$ つの領域に分割するので，$a_k=2$ です．いま平面に，条件を満たすような円が $k$ 個あるとします．$k+1$ 個目の円を条件を満たすように加えると，この円はもとの $k$ 個の円とそれぞれちょうど $2$ 回交わります．したがって，領域は新たに $2k$ 個増えます．ゆえに，次の漸化式が成り立ちます．
$$a_k=2$$ $$a_{k+1}=a_{k}+2k (k \ge 1)$$ これを解くと，$a_k=k^2-k+2$ となります．したがって，$n$ 個の円で分割できる領域の個数は多くとも $n^2-n+2$ 個です．ところが，集合が $n$ 個のとき，必要な領域の個数は $2^n$ 個であり，$n \ge 4$ のとき， $$2^n > n^2-n+2$$ が成り立つ (帰納法等で示せます) ので，円では分割できる領域の個数が足りず，ベン図が描けないことが示せました．
円では $4$ つ以上の集合のベン図を描けないことを上で示しましたが，円でない図形なら，描くことができる場合があります．ただし，あまり複雑すぎる図形を用いたり，それぞれの集合で異なる図形を用いたりすると，ベン図を描いても美しくなく，有用ではありません．
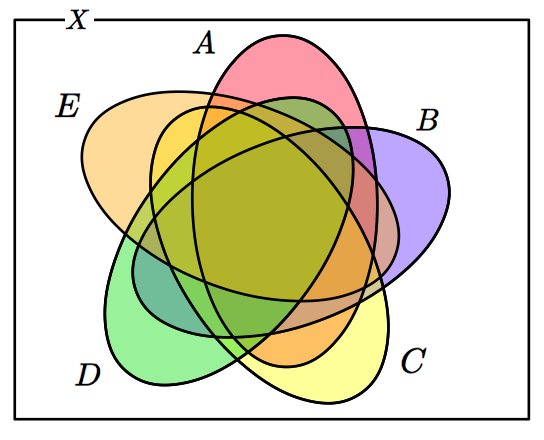
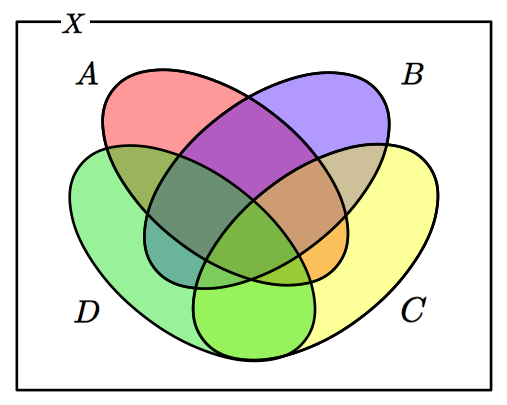
下の二つの図は，集合が $4$ つの場合と $5$ つの場合のベン図を，楕円を用いて表現しています．
$n=4$
$n=5$
