三角形の五心のひとつ,重心の性質について解説します.
三角形の頂点と,その向かい合う辺の中点を結んだ線分を中線と呼びます.三角形の $3$ つの中線はただひとつの点で交わり,その点を三角形の重心と呼びます.
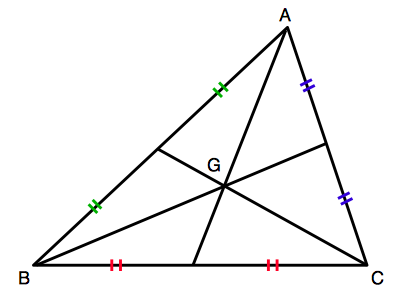
上の図で,$G$ が $△ABC$ の重心です.
重心の位置ベクトルは,$3$ 頂点の位置ベクトルの平均になります.
$△ABC$ の頂点 $A,B,C$ の位置ベクトルをそれぞれ $\vec{a},\vec{b},\vec{c}$ とすると,$△ABC$ の重心 $G$ の位置ベクトル $\vec{g}$ は,次の式 で表される. $$\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}$$
また,重心は各中線を $2:1$ に内分します.
いかなる三角形についても,その重心は三角形の内部にあります. ベクトルを用いて,そのことを説明します.点 $P$ の位置ベクトルを $\vec{p}$ とすると,点 $P$ が $△ABC$ の内部 (三角形の辺と頂点を含めない) にあるための条件は,$3$ つの条件 $0 < s < 1,0 < t < 1,0 < s+t < 1$ を満たす実数 $s,t$ を用いて, $$\vec{p}=s\overrightarrow{AB}+t\overrightarrow{AC}$$ と表せることです.
ここで,点 $A$ を始点と考える ($\vec{a}=\vec{0}$) と,$△ABC$ の重心 $G$ の位置ベクトル $\vec{g}$は, $$\vec{g}=\frac{1}{3}\vec{b}+\frac{1}{3}\vec{c}$$ $$=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$$ となるので,これは,$△ABC$ の内部にあるための条件を満たします.したがって,重心はつねに三角形の内部にあります.
ちなみに,三角形の五心のうち,常に三角形の内部にあるのは,重心と内心のみです.外心と垂心は三角形の内部にある場合と外部にある場合の両方があります.また,傍心は常に三角形の外部にあります.
中線によって,三角形は面積の等しい $2$ つの三角形に分割されます.
さらに,下の図のように各頂点と重心を結ぶ $3$ 直線によって,三角形は面積の等しい $3$ つの三角形に分割されます.
そして,下の図のように $3$ 中線によって,面積の等しい $6$ つの三角形に分割されます.
