組合せの問題ではよくあるマス目の彩色問題です．(今回は格子点の彩色と言っていますが，本質的にはマス目の彩色といっても同じです)
さて，$3\times 7$ の格子が与えられて，この $21$ 個の格子点それぞれに対して赤または青の色を割り当てることを考えます．
このとき，四隅が同色の長方形が必ず存在することを示すという問題です． つまり，赤または青をどのように割り当てたとしても，必ず四隅が赤のみの長方形か，あるいは四隅が青だけの長方形が必ず存在するのです．(正方形も当然長方形に含まれます)
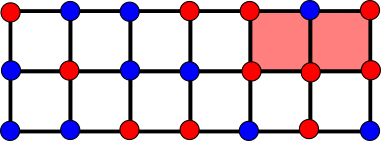実際に色の割り当てを適当に行ってみると，確かにこの主張が成り立ちそうな気がしてきます．
では，どのようにすればこの現象を数学的に示すことができるでしょうか？
考え方
単純にすべての色の割り当て方を考えると，(回転や裏返しで同じ塗り方となるものも区別すれば)$2^{21}=2097152$ 通りあります．これらひとつひとつの塗り方に対して，題意を満たすこと (つまり四隅が同色の長方形が必ず存在すること) を確かめるのは大変です．
そこで，どのような塗り方に対しても必ず成り立つ共通の性質を見つけ出す必要があります．鳩の巣原理が役に立ちそうです．
ヒント
つぎの性質に気づくことができればかなり見通しが良くなるでしょう． この問題では『一般性を失うことなく，行や列を任意に入れ替えてよい』です．つまり，ある色割り当てに対して，その行や列を好きなように入れ替えた色割り当てを考えます．このとき，『もとの色割り当てにおいて四隅が同色の長方形が存在するならば，入れ替えたあとの色割り当てでも四隅が同色の長方形が存在する』という事実が成り立ちます．
解答例
第 $1$ 行の $7$ つの格子点に対して，赤または青を割り当てることを考えます．鳩の巣原理より，どのような色割り当てを行っても赤または青の少なくともどちらか一方の色は $4$ つ以上の格子点に割り当てられるはずです．いま，仮に赤が割り当てられた格子点が $4$ つ以上あるとしましょう．(青としても同じです) 特に，任意の列を変更しても一般性は失われないので，第 $1,2,3,4$ 列の第 $1$ 行がすべて赤としてよいです．
ここで，第 $1,2,3,4$ 列の第 $2$ 行または第 $3$ 行に赤が割り当てられた格子点が $2$ つ以上あれば，明らかに題意を満たします．
そうではないとしましょう．すなわち，第 $1,2,3,4$ 列の第 $2$ 行と第 $3$ 行はそれぞれ赤が割り当てられた格子点がひとつ以下であるとしましょう．任意の列を変更しても一般性は失われないので，第 $1,2,3,4$ 列の中で，第 $2$ 行と第 $3$ 行に赤が割り当てられた格子点が存在しうる列を第 $1$ 列と第 $2$ 列としてよいです．
このとき，第 $3,4$ 列と第 $2,3$ 行の $4$ つの格子点はすべて青が割り当てられているはずなので，題意を満たします．
