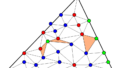
直角三角形 $ABC$ があり,$\triangle ABC$ の各辺と辺を共有するように $3$ つの正方形が接しています.このとき,六角形 $DEFGHI$ (下図の赤い部分)の面積を求めるのが問題です.
一見,簡単そうですが,きれいに解くためには頭を柔らかくする必要があります.
解答例
直角三角形 $ABC$ と $3$ つの正方形の面積はそれぞれ簡単に求めることができます.残る問題は,$\triangle CEF, \triangle AGH, \triangle BDI$ の面積を求めることです. 実は,これら $3$ つの三角形の面積はすべて $\triangle ABC$ の面積と等しいことが従います.
なぜなら,たとえば $\triangle ABC$ と $\triangle BDI$ の面積が等しいことはつぎのように説明できます.まず,下図のように,$\triangle ABC$ を $B$ を固定して時計回りに $90°$ 回転させます.この回転によって点 $A$ が移った位置を点 $A’$ とします.
$BC=BD$ なので,$C$ は $D$ の位置にきます.また,$\angle ABC+\angle DBI=180°$ なので,$3$ 点 $I, B, A’$ は同一直線上にあります.さらに,$IB = BA’$ なので,線分 $DB$ は $\triangle DA’I$ の中線です.
よって,$\triangle A’BD$ と $\triangle BDI$ は底辺と高さが等しいので面積が等しいことがわかります.当然 $\triangle A’BD$ と $\triangle ABC$ の面積も等しいので,$\triangle ABC$ と $\triangle BDI$ の面積が等しいことがわかります. 同様にして, $\triangle CEF, \triangle AGH$ の面積も $\triangle ABC$ の面積と等しいことがわかります.
以上より,六角形 $DEFGHI$ の面積は, $$9+16+25+6\times 4= \fbox{74}$$ となります.
回転移動に気づけるかどうかがポイントですね.