$3$ 倍角の公式とは $3\theta$ の正弦 (または余弦) を $\theta$ を用いて表す式です．三角関数のいろいろな公式の中でもややマニアックな公式になります．
$3$ 倍角の公式： $$・\large \sin 3\theta=3\sin \theta-4\sin^3 \theta$$ $$・\large \cos 3\theta=4\cos^3\theta-3\cos \theta$$
$3$ 倍角の公式は加法定理と $2$ 倍角の公式を用いればただちに導かれます．
証明：・$\underline{\sin 3\theta=3\sin \theta-4\sin^3 \theta}$ $$\sin 3\theta=\sin (\theta+2\theta)=\sin \theta \cos \theta+\cos \theta\sin 2\theta$$ $$=\sin \theta(1-2\sin^2 \theta)+\cos \theta(2\sin \theta\cos \theta)$$ $$=\sin \theta(1-2\sin^2 \theta)+2\sin \theta(1-\sin^2\theta)$$ $$=3\sin \theta-4\sin^3 \theta$$ ・$\underline{\cos 3\theta=4\cos^3\theta-3\cos \theta}$
$$\cos 3\theta=\cos (\theta+2\theta)=\cos \theta\cos 2\theta-\sin \theta\sin 2\theta$$ $$=\cos \theta(2\cos^2 \theta-1)-\sin \theta(2\sin \theta\cos \theta)$$ $$=\cos \theta(2\cos^2 \theta-1)-2(1-\cos^2 \theta)\cos \theta$$ $$=4\cos^3 \theta-3\cos \theta$$
また，$2$ 倍角の公式と同様に，ド・モアブルの定理を用いて示すこともできます．
ド・モアブルの定理を用いた証明： ド・モアブルの定理より， $$(\cos 3\theta+i\sin 3\theta)=(\cos \theta+i\sin \theta)^3$$ が成り立つ．ここで，右辺を計算すると， $$(右辺)=\cos^3 \theta+3\cos ^2\theta(i\sin \theta)+3\cos \theta(i \sin \theta)^2+(i\sin \theta)^3$$ $$=(\cos ^3 \theta-3\cos \theta \sin ^2\theta)+i(3\cos^2\theta\sin \theta-\sin^3\theta)$$ $$=(4\cos^3 \theta-3\cos \theta)+i(3\sin \theta-4\sin^3 \theta)$$ となる．これと，もとの式の左辺について実部と虚部を比較すれば，$3$ 倍角の公式が得られる．
三角関数のいろいろな公式は，角度 $\theta$ のとりうる範囲を制限すれば，図形的に導くことができます．
$0 下図のように，$AB=AC=1,\angle BAC=2\theta,\angle CAD=\theta,\angle ADB=\frac{\pi}{2}$ となる図形を用意します．また，$AC$ と $BD$ の交点を $E$ とします．
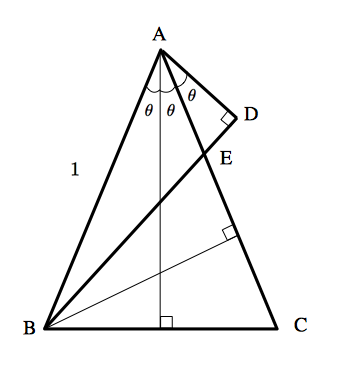$AD$ と $BD$ をそれぞれ $2$ 通りの方法で表すことによって，$3$ 倍角の公式を導きます． まず，$△ABD$ に注目すると，三角比の定義から， $$AD=\cos 3\theta$$ $$BD=\sin 3\theta$$ です．
ここで， $$\angle EBC=\angle ABC-\angle ABD=\frac{\pi-2\theta}{2}-\left(\pi-(3\theta+\frac{\pi}{2})\right)=2\theta$$ です．一方，$\angle ACB=\frac{\pi-2\theta}{2}$ なので，$△BCE$ は $BC=BE$ の二等辺三角形となります．
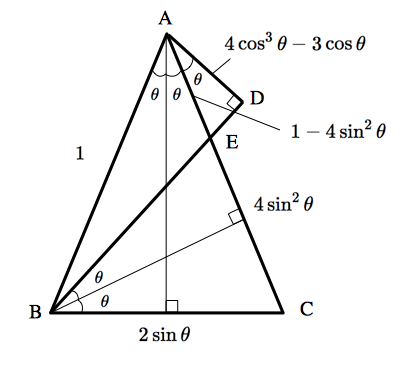
さて，まずは $AD$ の長さを $\cos \theta$ の式で表します．$BC→CE→AE→AD$ の順に辺の長さを求めていきます． $$BC=AB\times \sin \theta\times 2=2\sin \theta$$ $$CE=BC\times \sin \theta \times 2=4\sin^2 \theta$$ $$AE=AC-CE=1-4\sin^2 \theta$$ よって， $$AD=AE\times \cos \theta=(1-4\sin^2 \theta)\cos \theta=4\cos^3 \theta-3\cos \theta$$ です．
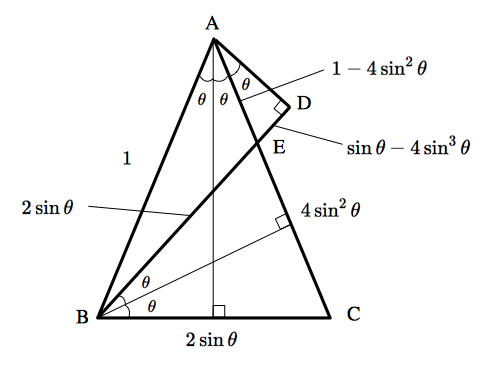
つぎに，$BD$ の長さを $\sin \theta$ の式で表します． $$BE=BC=2\sin^2 \theta$$ $$ED=AE\times \sin \theta=\sin \theta-4\sin^3 \theta$$ よって， $$BD=BE+ED=2\sin^2 \theta+\sin \theta-4\sin^3 \theta=3\sin \theta-4\sin^3 \theta$$ です．
以上より，$0
